
【题目】已知△ABC的一条边BC的长为5,另两边AB,AC的长分别为关于x的一元二次方程![]() 的两个实数根。
的两个实数根。
(1)求证:无论k为何值,方程总有两个不相等的实数根;
(2)当k=2时,请判断△ABC的形状并说明理由;
(3)k为何值时,△ABC是等腰三角形,并求△ABC的周长。
【答案】(1)见解析;(2)△ABC为直角三角形,见解析;(3)当k=4时,△ABC是等腰三角形,△ABC的周长=16;当k=3时,△ABC是等腰三角形,△ABC的周长=14.
【解析】
(1)根据根的判别式即可求出答案;
(2)将k的值代入原方程并求解后,根据勾股定理逆定理即可求出答案;
(3)根据等腰三角形的性质即可求出k的值.
(1)△=(2k+3)2-4(k2+3k+2)=1>0,
∴无论k为何值,方程总有两个不相等的实数根;
(2)当k=2时,
∴原方程化为:x2-7x+12=0,
解得:x=3或x=4,
∴32+42=52,
∴△ABC是直角三角形;
(3)当BC是等腰三角形的腰时,
∴x=5是方程的x2-(2k+3)x+k2+3k+2=0解,
∴25-5(2k+3)+k2+3k+2=0,
解得:k2-7k+12=0,
∴k=3或k=4,
若k=3时,
则方程为:x2-9x+20=0,
∴x=4或x=5,满足三角形三边关系,
此时周长为14;
若k=4时,
则方程:x2-11x+30=0,
∴x=5或x=6,满足三角形三边关系,
此时周长为16;
当BC是等腰三角形的底边时,
此时方程的x2-(2k+3)x+k2+3k+2=0有两个相等的解,不满足题意,
综上所述,△ABC的周长为14或16.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交点C,抛物线
与x轴交于点A,与y轴交点C,抛物线![]() 过A,C两点,与x轴交于另一点B.
过A,C两点,与x轴交于另一点B.
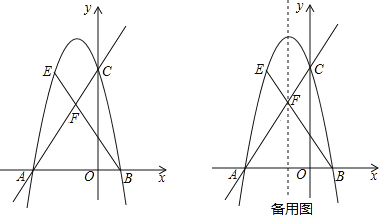
(1)求抛物线的解析式.
(2)在直线AC上方的抛物线上有一动点E,连接BE,与直线AC相交于点F,当![]() 时,求
时,求![]() 的值.
的值.
(3)点N是抛物线对称轴上一点,在(2)的条件下,若点E位于对称轴左侧,在抛物线上是否存在一点M,使以M,N,E,B为顶点的四边形是平行四边形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴于A,反比例函数y=![]() (x>0)的图象经过点C,交AB于点D,已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D,已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值.
(2)连接OC,若AD=AC,求CO的长.
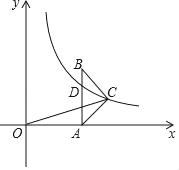
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个三角形,设其三个内角度数分别为![]() ,
,![]() 和
和![]() ,若x,y,z满足
,若x,y,z满足![]() ,我们定义这个三角形为美好三角形.
,我们定义这个三角形为美好三角形.
(1)△ABC中,若![]() ,
,![]() ,则△ABC (填”是”或”不是”)美好三角形;
,则△ABC (填”是”或”不是”)美好三角形;
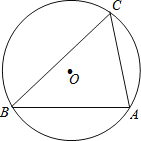
(2)如图,锐角△ABC是⊙O的内接三角形,![]() ,
,![]() ,⊙O直径为
,⊙O直径为![]() ,求证:△ABC为美好三角形;
,求证:△ABC为美好三角形;
(3)已知△ABC为美好三角形,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
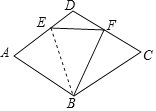
【题目】如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:
①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE![]() S菱形ABCD
S菱形ABCD
下列判断正确的是( )
A. ①,②都对B. ①,②都错C. ①对,②错D. ①错,②对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长40cm、宽24cm的矩形纸板,将纸板四个角各剪去一个边长为xcm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.
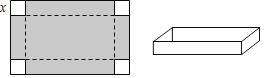
(1)这个无盖纸盒的长为 cm,宽为 cm;(用含x的式子表示)
(2)若要制成一个底面积是720 ![]() 的无盖长方体纸盒,求x的值.
的无盖长方体纸盒,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()
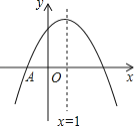
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
入住的房间数量 | 房间价格 | 总维护费用 | |
提价前 | 60 | 200 | 60×20 |
提价后 |
|
|
|
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙I是△ABC的内切圆,切点分别是D、E、F.
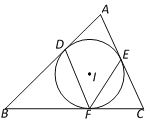
(1)若∠B=50°,∠C=70°,则∠DFE的度数为 ;
(2)若∠DFE=50°,求∠A的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com