
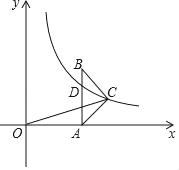
【题目】如图,在△ABC中,AC=BC,AB⊥x轴于A,反比例函数y=![]() (x>0)的图象经过点C,交AB于点D,已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D,已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值.
(2)连接OC,若AD=AC,求CO的长.
【答案】(1)k=11;(2)![]()
【解析】试题分析:(1)利用等腰三角形的性质得出AE,BE的长,再利用勾股定理得出OA的长,得出C点坐标即可得出答案;
(2)首先表示出D,C点坐标进而利用反比例函数图象上的性质求出C点坐标,再利用勾股定理得出CO的长.
试题解析:解:(1)作CE⊥AB,垂足为E.∵AC=BC,AB=4,∴AE=BE=2.
在Rt△BCE中,BC=![]() ,BE=2,∴CE=
,BE=2,∴CE=![]() .∵OA=4,∴C点的坐标为:(
.∵OA=4,∴C点的坐标为:(![]() ,2).∵点C在y=
,2).∵点C在y=![]() (x>0)的图象上,∴k=11;
(x>0)的图象上,∴k=11;
(2)设A点的坐标为(m,0).∵BD=BC=![]() ,∴AD=
,∴AD=![]() ,∴D,C两点的坐标分别为:(m,
,∴D,C两点的坐标分别为:(m,![]() ),(m+
),(m+![]() ,2).
,2).
∵点C,D都在y=![]() (x>0)的图象上,∴
(x>0)的图象上,∴![]() m=2(m+
m=2(m+![]() ),∴m=6,∴C点的坐标为:(
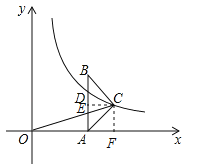
),∴m=6,∴C点的坐标为:(![]() ,2),作CF⊥x轴,垂足为F,∴OF=
,2),作CF⊥x轴,垂足为F,∴OF=![]() ,CF=2.在Rt△OFC中,OC2=OF2+CF2,∴OC=
,CF=2.在Rt△OFC中,OC2=OF2+CF2,∴OC=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知长方形ABCD中AB = 8cm,BC = 10cm,在边CD上取一点E,将△ADE折叠,使点D恰好落在BC边上的点F,则CF的长为( )
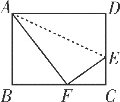
A. 2cm B. 3cm C. 4cm D. 5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
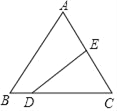
【题目】如图,等边△ABC的边长为8,D、E两点分别从顶点B、C出发,沿边BC、CA以1个单位/s、2个单位/s的速度向顶点C、A运动,DE的垂直平分线交BC边于F点,若某时刻tan∠CDE=![]() 时,则线段CF的长度为_____.
时,则线段CF的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地相距
两地相距![]() ,
,![]() 地在
地在![]() 、
、![]() 两地之间.一辆轿车以
两地之间.一辆轿车以![]() 的速度从
的速度从![]() 地出发匀速行驶,前往
地出发匀速行驶,前往![]() 地.同时,一辆货车以
地.同时,一辆货车以![]() 的速度从
的速度从![]() 地出发,匀速行驶,前往
地出发,匀速行驶,前往![]() 地.
地.
(1)当两车相遇时,求轿车行驶的时间;
(2)当两车相距![]() 时,求轿车行驶的时间.
时,求轿车行驶的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晨光文具店的某种毛笔每支售价30元,书法纸每本售价10元.为促销制定了两种优惠方案:甲方案,买一支毛笔就送一本书法纸;乙方案,按购买的总金额打8折.某校欲为书法小组购买这种毛笔10支,书法纸x(x≥10)本.
(1)求甲方案实际付款金额![]() 元与x的函数关系式和乙方案实际付款金额
元与x的函数关系式和乙方案实际付款金额![]() 元与x的函数关系式;
元与x的函数关系式;
(2)试通过计算为该校提供一种节约费用的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是线段AB上任一点,AB=12 cm,C、D两点分别从P、B同时向A点运动,且C点的运动速度为2 cm/s,D点的运动速度为3 cm/s,运动的时间为t s.
![]()
(1)若AP=8 cm.
①运动1 s后,求CD的长;
②当D在线段PB运动上时,试说明AC=2CD;
(2)如果t=2 s时,CD=1 cm,试探索AP的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com