
【题目】晨光文具店的某种毛笔每支售价30元,书法纸每本售价10元.为促销制定了两种优惠方案:甲方案,买一支毛笔就送一本书法纸;乙方案,按购买的总金额打8折.某校欲为书法小组购买这种毛笔10支,书法纸x(x≥10)本.
(1)求甲方案实际付款金额![]() 元与x的函数关系式和乙方案实际付款金额
元与x的函数关系式和乙方案实际付款金额![]() 元与x的函数关系式;
元与x的函数关系式;
(2)试通过计算为该校提供一种节约费用的购买方案.
【答案】(1)y甲=10x+200(x≥10);![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)甲方案实际付款=10支毛笔的价钱+10本以外练习本的总价钱,把相关数值代入即可求解;乙方案实际付款=(10支毛笔的总价钱+练习本的总价钱)×0.8,把相关数值代入即可求解;
(2)把①②得到的式子比较大小列出式子计算即可.
解:(1)①![]() =30×10+10(x-10)=10x+200(x≥10);
=30×10+10(x-10)=10x+200(x≥10);
②![]() =(30×10+10x)×0.8=8x+240;
=(30×10+10x)×0.8=8x+240;
(2)①∵10x+200>8x+240,
解得:x>20;
∴当练习本超过20本时,选择乙方案;
②∵10x+200=8x+240,
解得:x=20;
∴当练习本为20本时,两种方案价钱一样;
③∵10x+200<8x+240,
解得:x<20;
∴当练习本少于20本时,选择甲方案.
答:当练习本超过20本时,选择乙方案;当练习本为20本时,两种方案价钱一样;当练习本少于20本时,选择甲方案.


科目:初中数学 来源: 题型:
【题目】甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量![]() (个)与加工时间
(个)与加工时间![]() (分)之间的函数关系,观察图象解决下列问题:
(分)之间的函数关系,观察图象解决下列问题:
(1)点B的坐标是________,B点表示的实际意义是___________ _____;
(2)求线段BC对应的函数关系式和D点坐标;
(3)乙在加工的过程中,多少分钟时比甲少加工100个零件?
(4)为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少分钟时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
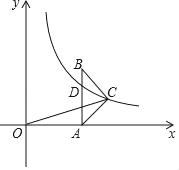
【题目】如图,在△ABC中,AC=BC,AB⊥x轴于A,反比例函数y=![]() (x>0)的图象经过点C,交AB于点D,已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D,已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值.
(2)连接OC,若AD=AC,求CO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径。
(1)如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段AC,同时我们还发现损矩形中有公共边的两个三角形角的特点,在公共边的同侧的两个角是相等的。如图1中:△ABC和△ABD有公共边AB,在AB同侧有∠ADB和∠ACB,此时∠ADB=∠ACB;再比如△ABC和△BCD有公共边BC,在CB同侧有∠BAC和∠BDC,此时∠BAC=∠BDC。请再找一对这样的角来 =
(2)如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由。
(3)在第(2)题的条件下,若此时AB=![]() ,BD=
,BD=![]() ,求BC的长。
,求BC的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
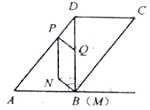
【题目】如图,BD是□ABCD的对角线,AB⊥BD,BD=8cm,AD=10cm,动点P从点D出发,以5cm/s的速度沿DA运动到终点A,同时动点Q从点B出发,沿折线BD—DC运动到终点C,在BD、DC上分别以8cm/s、6cm/s的速度运动.过点Q作QM⊥AB,交射线AB于点M,连接PQ,以PQ与QM为边作□PQMN.设点P的运动时间为t(s)(t>0),□PQMN与□ABCD重叠部分图形的面积为S(cm2).
(1)AP=_______cm(同含t的代数式表示).
(2)当点N落在边AB上时,求t的值.
(3)求S与t之间的函数关系式.
(4)连结NQ,当NQ与△ABD的一边平行时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
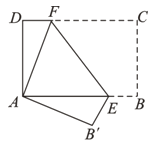
【题目】如图,将矩形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F, 点B的对应点为B′.
(1)证明:AE=CF;
(2)若AD=12,DC=18,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在黄金周促销期间规定:商场内所有商品按标价的![]() 打折出售;同时,当顾客在该商场消费打折后的金额满一定数额,还可按如下方案抵扣相应金额:
打折出售;同时,当顾客在该商场消费打折后的金额满一定数额,还可按如下方案抵扣相应金额:
打折后消费金额 |
|
|
|
|
|
抵扣金额 | 20 | 30 | 40 | 50 |
|
说明:![]() 表示在范围
表示在范围![]() 中,可以取到a,不能取到b.
中,可以取到a,不能取到b.
根据上述促销方法,顾客在该商场购物可以获得双重优惠:打折优惠与抵扣优惠.
例如:购买标价为900元的商品,则打折后消费金额为450元,获得的抵扣金额为30元,总优惠额为:![]() 元,实际付款420元.
元,实际付款420元.![]() 购买商品得到的优惠率
购买商品得到的优惠率![]()
请问:
![]() 购买一件标价为500元的商品,顾客的实际付款是多少元?
购买一件标价为500元的商品,顾客的实际付款是多少元?
![]() 购买一件商品,实际付款375元,那么它的标价为多少元?
购买一件商品,实际付款375元,那么它的标价为多少元?
![]() 请直接写出,当顾客购买标价为______元的商品,可以得到最高优惠率为______.
请直接写出,当顾客购买标价为______元的商品,可以得到最高优惠率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车厂计划半年内每月生产汽车20辆,由于另有任务,每月上班人数不一定相等,实每月生产量与计划量相比情况如下表(增加为正,减少为负)

(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)半年内总生产量是多少?比计划多了还是少了,增加或减少多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于一次函数y=﹣2x+3,下列结论正确的是( )
A. 图象过点(1,﹣1) B. 图象经过一、二、三象限
C. y随x的增大而增大 D. 当x>![]() 时,y<0
时,y<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com