
【题目】定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径。
(1)如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段AC,同时我们还发现损矩形中有公共边的两个三角形角的特点,在公共边的同侧的两个角是相等的。如图1中:△ABC和△ABD有公共边AB,在AB同侧有∠ADB和∠ACB,此时∠ADB=∠ACB;再比如△ABC和△BCD有公共边BC,在CB同侧有∠BAC和∠BDC,此时∠BAC=∠BDC。请再找一对这样的角来 =
(2)如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由。
(3)在第(2)题的条件下,若此时AB=![]() ,BD=
,BD=![]() ,求BC的长。
,求BC的长。

【答案】(1)∠ABD=∠ACD;(2)四边形ACEF为正方形,理由见解析;(3)5.
【解析】
(1)以AD为公共边,有∠ABD=∠ACD;
(2)证明△ADC是等腰直角三角形,得AD=CD,则AE=CF,根据对角线相等的菱形是正方形可得结论;
(3)如图2,作辅助线构建直角三角形,证明△ABC≌△CHE,得CH=AB=3,根据平行线等分线段定理可得BG=GH=4,从而得结论.
解:(1)由图1得:△ABD和△ADC有公共边AD,在AD同侧有∠ABD和∠ACD,此时∠ABD=∠ACD;
(2)四边形ACEF为正方形,理由是:
∵∠ABC=90°,BD平分∠ABC,
∴∠ABD=∠CBD=45°
∴∠DAC=∠CBD=45°
∵四边形ACEF是菱形,
∴AELCF,
∴∠ADC=90°,
∴△ADC是等腰直角三角形,
∴AD=CD,.AE=CF,
∴菱形ACEF是正方形;
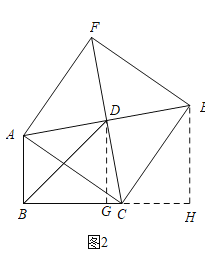
(3)如图2,过D作DG⊥BC于G,过E作EH⊥BC,交BC的延长线于H,
∵∠DBG=45°,
∴△BDG是等腰直角三角形,BD=4![]() ,
,
∵BG=4,四边形ACEF是正方形,
∴AC=CE,∠ACE=90°,AD=DE,
易得△ABC≌△CHE,
∴CH=AB=3,AB//DG//EH,AD=DE,
∴BG=GH=4,
∴CG=4-3=1,
∴BC=BG+CG=4+1=5.


科目:初中数学 来源: 题型:
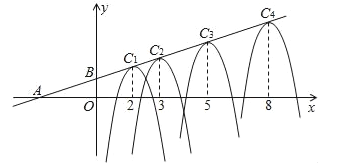
【题目】如图,在平面直角坐标系xoy中,A(﹣3,0),B(0,1),形状相同的抛物线Cn(n=1,2,3,4,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…,根据上述规律,抛物线C2的顶点坐标为_____;抛物线C8的顶点坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
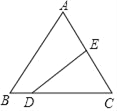
【题目】如图,等边△ABC的边长为8,D、E两点分别从顶点B、C出发,沿边BC、CA以1个单位/s、2个单位/s的速度向顶点C、A运动,DE的垂直平分线交BC边于F点,若某时刻tan∠CDE=![]() 时,则线段CF的长度为_____.
时,则线段CF的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
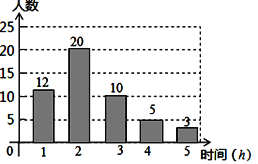
【题目】珠海市某中学在创建“书香校园”活动中,为了解学生的读书情况,某校抽样调查了部分同学在一周内的阅读时间,绘制如下统计图.根据图中信息,解答下列问题:
(1)被抽查学生阅读时间的中位数为 h,平均数为 h;
(2)若该校共有1500名学生,请你估算该校一周内阅读时间不少于3h的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晨光文具店的某种毛笔每支售价30元,书法纸每本售价10元.为促销制定了两种优惠方案:甲方案,买一支毛笔就送一本书法纸;乙方案,按购买的总金额打8折.某校欲为书法小组购买这种毛笔10支,书法纸x(x≥10)本.
(1)求甲方案实际付款金额![]() 元与x的函数关系式和乙方案实际付款金额
元与x的函数关系式和乙方案实际付款金额![]() 元与x的函数关系式;
元与x的函数关系式;
(2)试通过计算为该校提供一种节约费用的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AB=18,cosB=![]() ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )
A. 6![]() B. 7
B. 7![]() C. 8
C. 8![]() D. 9
D. 9![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
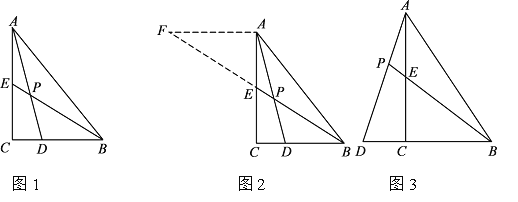
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com