
【题目】如图是一张长40cm、宽24cm的矩形纸板,将纸板四个角各剪去一个边长为xcm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.
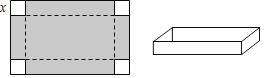
(1)这个无盖纸盒的长为 cm,宽为 cm;(用含x的式子表示)
(2)若要制成一个底面积是720 ![]() 的无盖长方体纸盒,求x的值.
的无盖长方体纸盒,求x的值.
【答案】(1)40-2x, 24-2x;(2)x的值为2.
【解析】
(1)根据矩形纸板的长、宽,结合剪去正方形的边长可得出无盖纸盒的长、宽;
(2)根据矩形的面积公式结合无盖长方体纸盒的底面积为720cm2,即可得出关于x的一元二次方程,解之取其较小值即可得出结论.
解:(1)∵纸板是长为40cm,宽为24cm的矩形,且纸板四个角各剪去一个边长为xcm的正方形,
∴无盖纸盒的长为(40-2x)cm,宽为(24-2x)cm.
故答案为:40-2x, 24-2x;
(2)依题意,得:(40-2x)(24-2x)=720,
解得:x1=2,x2=30(不合题意,舍去).
答:x的值为2.
故答案为:(1)40-2x, 24-2x;(2)x的值为2.


科目:初中数学 来源: 题型:
【题目】把二次涵数![]() 的图象先向左平移2个单位长度,再向上平移4个单位长度,得到二次函数
的图象先向左平移2个单位长度,再向上平移4个单位长度,得到二次函数![]() 的图象.
的图象.
(1)试确定![]() ,
,![]() ,
,![]() 的值;
的值;
(2)指出二次函数![]() 图象的开口方向、对称轴和顶点坐标.
图象的开口方向、对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在平行四边形纸片ABCD中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC折叠得到△AB'C.
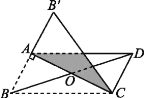
(1)求证:以A、C、D、B'为顶点的四边形是矩形
(2)若四边形ABCD的面积S=12cm,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的一条边BC的长为5,另两边AB,AC的长分别为关于x的一元二次方程![]() 的两个实数根。
的两个实数根。
(1)求证:无论k为何值,方程总有两个不相等的实数根;
(2)当k=2时,请判断△ABC的形状并说明理由;
(3)k为何值时,△ABC是等腰三角形,并求△ABC的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,… 组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2019秒时,点P的坐标是( )
个单位长度,则第2019秒时,点P的坐标是( )
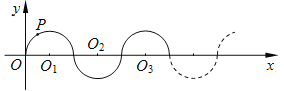
A. (2018,0)B. (2019,![]() 1)C. (2019,1)D. (2018,-1)
1)C. (2019,1)D. (2018,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
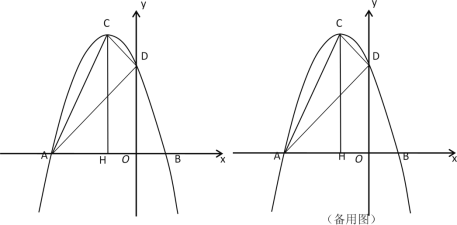
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
(1)求抛物线的解析式和顶点C的坐标;
(2)连结AD、CD,若点E为抛物线上一动点(点E与顶点C不重合),当△ADE与△ACD面积相等时,求点E的坐标;
(3)若点P为抛物线上一动点(点P与顶点C不重合),过点P向CD所在的直线作垂线,垂足为点Q,以P、C、Q为顶点的三角形与△ACH相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于_____.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923101670465536/1923902127538176/STEM/3534c7f6f1a5489684ae6308493b71da.png]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com