
【题目】如图.在平行四边形纸片ABCD中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC折叠得到△AB'C.
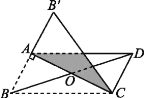
(1)求证:以A、C、D、B'为顶点的四边形是矩形
(2)若四边形ABCD的面积S=12cm,求阴影部分的面积.
【答案】(1)见解析;(2)阴影部分的面积是3.
【解析】
(1)连接B'D,由平行四边形的性质及折叠性质可得AB'=CD,∠BAC=∠B'AC,由AC⊥AB可证明B、A、B'共线,可得AB′//CD,可证明四边形ACDB'为平行四边形,根据有一个角是90°的平行四边形是矩形即可证明以A、C、D、B'为顶点的四边形是矩形;(2)设B'C与AD交于点E,根据矩形的性质可得AE=DE,由平行四边形的性质可得S△ACD=![]() S平行四边形ABCD,根据等底等高的三角形面积相等可得S△AEC=
S平行四边形ABCD,根据等底等高的三角形面积相等可得S△AEC=![]() S△ACD,即可求出阴影部分面积.
S△ACD,即可求出阴影部分面积.
(1)连接B'D.
∵在ABCD中,AB=CD,AB∥CD,△ABC沿对角线AC折叠,
∴AB'=CD,∠BAC=∠B'AC.
又∵AC⊥AB,
∴∠BAC=∠B'AC=90°,
∴B、A、B'在一条直线上,
∴AB'∥CD,
∴四边形ACDB'为平行四边形,
∵∠B'AC=90°,
∴以A、C、D、B'为顶点的四边形是矩形.
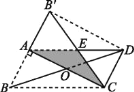
(2)设B'C与AD交于点E.
∵四边形ABCD是平行四边形,S平行四边形ABCD=12cm,
∴S△ACD=![]() S平行四边形ABCD=
S平行四边形ABCD=![]() ×12=6,
×12=6,
∵四边形ACDB'为矩形,
∴AE=DE,
∴S△AEC=![]() S△ACD=
S△ACD=![]() ×6=3,即阴影部分的面积是3.
×6=3,即阴影部分的面积是3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】佳佳文具店购进A,B两种款式的笔袋,其中A种笔袋的单价比B种袋的单价低10%.已知店主购进A种笔袋用了810元,购进B种笔袋用了600元,且所购进的A种笔袋的数量比B种笔袋多20个.请问:文具店购进A,B两种款式的笔袋各多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
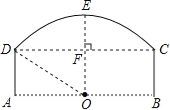
【题目】如图为一桥洞的形状,其正视图是由圆弧![]() 和矩形ABCD构成.O点为
和矩形ABCD构成.O点为![]() 所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F)EF为2米.
所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F)EF为2米.
(1)求![]() 所在⊙O的半径DO;
所在⊙O的半径DO;
(2)若河里行驶来一艘正视图为矩形的船,其宽6米,露出水面AB的高度为h米,求船能通过桥洞时的最大高度h.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个三角形,设其三个内角度数分别为![]() ,
,![]() 和
和![]() ,若x,y,z满足
,若x,y,z满足![]() ,我们定义这个三角形为美好三角形.
,我们定义这个三角形为美好三角形.
(1)△ABC中,若![]() ,
,![]() ,则△ABC (填”是”或”不是”)美好三角形;
,则△ABC (填”是”或”不是”)美好三角形;
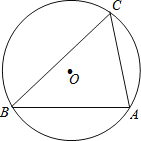
(2)如图,锐角△ABC是⊙O的内接三角形,![]() ,
,![]() ,⊙O直径为
,⊙O直径为![]() ,求证:△ABC为美好三角形;
,求证:△ABC为美好三角形;
(3)已知△ABC为美好三角形,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校新初三暑期阅读课外书的情况,某研究小组随机采访该校新九年级的20位同学,得到这20位同学暑期读课外书册数的统计如下:
册数 | 0 | 2 | 3 | 5 | 6 | 8 | 10 |
人数 | 1 | 2 | 4 | 8 | 2 | 2 | 1 |
(1)这20位同学暑期看课外书册数的中位数是 册,众数是 册,平均数是 册。
(2)若小明同学把册数中的数据“8”看成了“7”,那么中位数,众数,平均数中不受影响的是。
(3)若该校有600名新初三学生,试估计该校新初三学生暑期阅读课外书的总册数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长40cm、宽24cm的矩形纸板,将纸板四个角各剪去一个边长为xcm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.
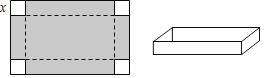
(1)这个无盖纸盒的长为 cm,宽为 cm;(用含x的式子表示)
(2)若要制成一个底面积是720 ![]() 的无盖长方体纸盒,求x的值.
的无盖长方体纸盒,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬天来了,晒衣服成了头疼的事情,聪明的小华想到一个好办法,在家后院地面(BD)上立两根等长的立柱AB、CD(均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线y=ax2-0.8x+c,如图1,已知立柱AB=CD=2.6米,BD=8米.
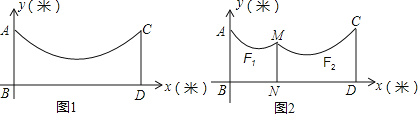
(1)求绳子最低点离地面的距离;
(2)为了防止衣服碰到地面,小华在离AB为3米的位置处用一根垂直于地面的立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.6米,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,∠ABC=45°,OC∥AD,AD交BC的延长线于D,AB交OC于E.

(1)求证:AD是⊙O的切线;
(2)若⊙O的直径为6,线段BC=2,求∠BAC的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com