
【题目】冬天来了,晒衣服成了头疼的事情,聪明的小华想到一个好办法,在家后院地面(BD)上立两根等长的立柱AB、CD(均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线y=ax2-0.8x+c,如图1,已知立柱AB=CD=2.6米,BD=8米.
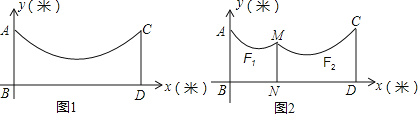
(1)求绳子最低点离地面的距离;
(2)为了防止衣服碰到地面,小华在离AB为3米的位置处用一根垂直于地面的立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.6米,求MN的长.
【答案】(1)1米;(2)1.85米
【解析】
(1)根据题意可以求出抛物线的解析式,从而可以求得抛物线的顶点坐标,进而得到绳子最低点离地面的距离;
(2)根据题意可以求得抛物线F1的函数解析式,然后将x=3代入求出的函数解析式即可解答本题.
(1)∵抛物线经过点A(0,2.6)、C(8,2.6),∴![]() ,解得:a=0.1,c=2.6,∴y=0.1x2﹣0.8x+2.6=0.1(x﹣4)2+1,∴当x=4时,y取得最小值,此时y=1,即绳子最低点离地面的距离1米;
,解得:a=0.1,c=2.6,∴y=0.1x2﹣0.8x+2.6=0.1(x﹣4)2+1,∴当x=4时,y取得最小值,此时y=1,即绳子最低点离地面的距离1米;
(2)由题意可得:抛物线F1的顶点坐标为(2,1.6),设抛物线F1的函数解析式为y=a1(x﹣2)2+1.6.
∵点A(0,2.6)在抛物线F1上,∴2.6=a1(0﹣2)2+1.6,解得:a1=0.25,∴抛物线F1的函数解析式为y=0.25(x﹣2)2+1.6,当x=3时,y=0.25(3﹣2)2+1.6=1.85,即MN的长是1.85米.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax+bx+c与x轴的两个交点为B(1,0)和C,与y轴的交点坐标为(0,-1.5)且此抛物线过点A(3,6).

(1)求此二次函数的解析式;
(2)设此抛物线的顶点为P,对称轴与线段AC相交于点Q,求点P和点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在平行四边形纸片ABCD中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC折叠得到△AB'C.
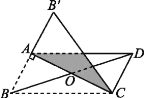
(1)求证:以A、C、D、B'为顶点的四边形是矩形
(2)若四边形ABCD的面积S=12cm,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,… 组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2019秒时,点P的坐标是( )
个单位长度,则第2019秒时,点P的坐标是( )
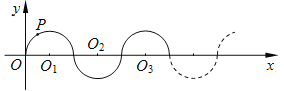
A. (2018,0)B. (2019,![]() 1)C. (2019,1)D. (2018,-1)
1)C. (2019,1)D. (2018,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
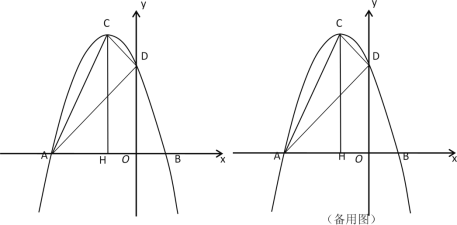
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
(1)求抛物线的解析式和顶点C的坐标;
(2)连结AD、CD,若点E为抛物线上一动点(点E与顶点C不重合),当△ADE与△ACD面积相等时,求点E的坐标;
(3)若点P为抛物线上一动点(点P与顶点C不重合),过点P向CD所在的直线作垂线,垂足为点Q,以P、C、Q为顶点的三角形与△ACH相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B![]() 90°,AB
90°,AB![]() 4,BC
4,BC![]() 2,以AC为边作△ACE,∠ACE
2,以AC为边作△ACE,∠ACE![]() 90°,AC=CE,延长BC至点D,使CD
90°,AC=CE,延长BC至点D,使CD![]() 5,连接DE.求证:△ABC∽△CED.
5,连接DE.求证:△ABC∽△CED.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于_____.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923101670465536/1923902127538176/STEM/3534c7f6f1a5489684ae6308493b71da.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线![]() 的顶点在拋物线
的顶点在拋物线![]() 上,抛物线
上,抛物线![]() 的顶点也在拋物线
的顶点也在拋物线![]() 上时,那么我们称抛物线
上时,那么我们称抛物线![]() 与
与![]() “互为关联”的抛物线.如图1,已知抛物线
“互为关联”的抛物线.如图1,已知抛物线![]() :
:![]() 与
与![]() :
:![]() 是“互为关联”的拋物线,点
是“互为关联”的拋物线,点![]() 分别是抛物线
分别是抛物线![]() ,
,![]() 的顶点,抛物线
的顶点,抛物线![]() 经过点
经过点![]() .
.
(1)直接写出![]() 的坐标和抛物线
的坐标和抛物线![]() 的解析式;
的解析式;
(2)抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 是直角三角形?如果存在,请求出点E的坐标;如果不存在,请说明理由;
是直角三角形?如果存在,请求出点E的坐标;如果不存在,请说明理由;
(3)如图2,点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 分别是抛物线
分别是抛物线![]() ,
,![]() 上的动点,且点
上的动点,且点![]() 的横坐标相同,记
的横坐标相同,记![]() 面积为
面积为![]() (当点
(当点![]() 与点
与点![]() 重合时
重合时![]() ),
),![]() 的面积为
的面积为![]() (当点
(当点![]() 与点
与点![]() 重合时,
重合时,![]() ),令
),令![]() ,观察图象,当
,观察图象,当![]() 时,写出
时,写出![]() 的取值范围,并求出在此范围内
的取值范围,并求出在此范围内![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a>0)的对称轴为x=-1,交x轴的一个交点为(x1,0),且0<x1<1, 则下列结论:①b>0,c<0;②a-b+c>0 ;③b<a ④ 3a+c>0,⑤9a-3b+c>0,其中正确的命题有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com