
【题目】如图,抛物线y=ax+bx+c与x轴的两个交点为B(1,0)和C,与y轴的交点坐标为(0,-1.5)且此抛物线过点A(3,6).

(1)求此二次函数的解析式;
(2)设此抛物线的顶点为P,对称轴与线段AC相交于点Q,求点P和点Q的坐标.
【答案】(1)抛物线的解析式为![]() ;(2)Q点的坐标为(-1,2), P的坐标为:(1,2).
;(2)Q点的坐标为(-1,2), P的坐标为:(1,2).
【解析】
(1)将A、B和(0,-1.5)代入二次函数y=ax+bx+c,联立方程组求出a、b、c即可得出函数解析式;
(2)由二次函数一般式可得函数顶点式从而求出二次函数的顶点坐标及对称轴方程,根据A,C两点的坐标可求出线段AC所在直线的表达式,由对称轴可得Q点横坐标,将x=1代入即可求出Q点纵坐标.
解:(1)根据题意把(1,0),(0,-1.5)和(3,6)代入y=ax+bx+c中得
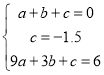 解得
解得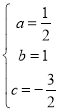 故此函数解析式为
故此函数解析式为![]() .
.
(2)由![]() .
.
∴抛物线顶点P的坐标为:(1,2),对称轴方程为:x=1.
设直线AC的方程为:y=k1x+b1.
∵A(3,6),C(3,0),
∴在该直线上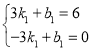 ,
,
解得![]() ,
,
直线AC的方程为:y=x+3
将x=1代入y=x+3得y=2,
∴Q点坐标为(1,2).


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
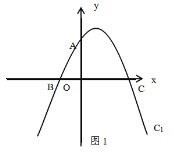
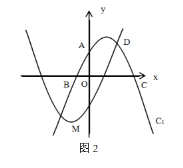
【题目】如图(1),在平面直角坐标系x Oy中,直线y=2x+4与y轴交于点A,与x轴交于点B,抛物线C1:y=![]() x2+bx+c过A,B两点,与x轴的另一交点为点C.
x2+bx+c过A,B两点,与x轴的另一交点为点C.
(1)求抛物线C1的解析式及点C的坐标;
(2)如图(2),作抛物线C2,使得抛物线C2与C1恰好关于原点对称,C2与C1在第一象限内交于点D,连接AD,CD,请直接写出抛物线C2的解析式和点D的坐标.
(3)已知抛物线C2的顶点为M,设P为抛物线C1对称轴上一点,Q为直线y=2x+4上一点,是否存在以点M,Q,P,B为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳佳文具店购进A,B两种款式的笔袋,其中A种笔袋的单价比B种袋的单价低10%.已知店主购进A种笔袋用了810元,购进B种笔袋用了600元,且所购进的A种笔袋的数量比B种笔袋多20个.请问:文具店购进A,B两种款式的笔袋各多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
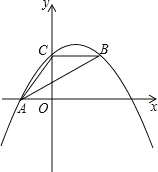
【题目】如图,抛物线y=ax2+bx+4 经过点A(﹣3,0),点 B 在抛物线上,CB∥x轴,且AB 平分∠CAO.则此抛物线的解析式是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
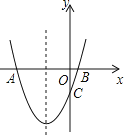
【题目】如图,抛物线y=x2+2x+k+1与x轴交与A、B两点,与y轴交与点C(0,-3).
(1)求抛物线的对称轴及k的值;
(2)求抛物线的对称轴上存在一点P,使得PA+PC的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标.
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为一桥洞的形状,其正视图是由圆弧![]() 和矩形ABCD构成.O点为
和矩形ABCD构成.O点为![]() 所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F)EF为2米.
所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F)EF为2米.
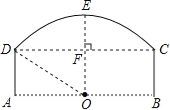
(1)求![]() 所在⊙O的半径DO;
所在⊙O的半径DO;
(2)若河里行驶来一艘正视图为矩形的船,其宽6米,露出水面AB的高度为h米,求船能通过桥洞时的最大高度h.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬天来了,晒衣服成了头疼的事情,聪明的小华想到一个好办法,在家后院地面(BD)上立两根等长的立柱AB、CD(均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线y=ax2-0.8x+c,如图1,已知立柱AB=CD=2.6米,BD=8米.
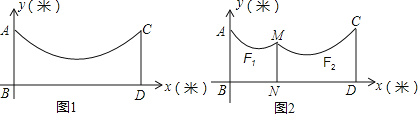
(1)求绳子最低点离地面的距离;
(2)为了防止衣服碰到地面,小华在离AB为3米的位置处用一根垂直于地面的立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.6米,求MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com