
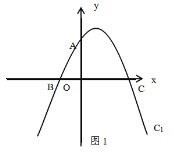
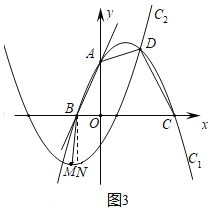
【题目】如图(1),在平面直角坐标系x Oy中,直线y=2x+4与y轴交于点A,与x轴交于点B,抛物线C1:y=![]() x2+bx+c过A,B两点,与x轴的另一交点为点C.
x2+bx+c过A,B两点,与x轴的另一交点为点C.
(1)求抛物线C1的解析式及点C的坐标;
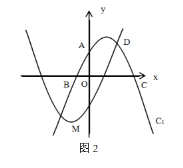
(2)如图(2),作抛物线C2,使得抛物线C2与C1恰好关于原点对称,C2与C1在第一象限内交于点D,连接AD,CD,请直接写出抛物线C2的解析式和点D的坐标.
(3)已知抛物线C2的顶点为M,设P为抛物线C1对称轴上一点,Q为直线y=2x+4上一点,是否存在以点M,Q,P,B为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2+
x2+![]() x+4,C(8,0);
x+4,C(8,0);
(2)y=![]() x2+
x2+![]() x-4,D(4,6);
x-4,D(4,6);
(3)(3,![]() )或(3,
)或(3,![]() );
);
【解析】
(1)先求出直线y=2x+4与x轴、y轴交点坐标,待定系数法求抛物线解析式即可;
(2)根据两抛物线关于原点对称,将抛物线C1的解析式中的x和y分别换成-x和-y,整理后即为抛物线C2的解析式;再通过解方程组求点D的坐标;
(3)过B作BN∥y轴,过M作MN∥x轴与BN交于点N,分两种情形分别求点P的坐标:①BM为平行四边形的边,②BM为平行四边形的对角线.
(1)∵直线y=2x+4与y轴交于点A,与x轴交于点B,∴A(0,4),B(-2,0),
∵抛物线C1:y=-![]() x2+bx+c过A,B两点,
x2+bx+c过A,B两点,
∴c=4,0=-![]() ×(-2)2-2b+4,解得b=
×(-2)2-2b+4,解得b=![]()
∴抛物线C1的解析式为:y=-![]() x2+
x2+![]() x+4
x+4
令y=0,得-![]() x2+
x2+![]() x+4=0,解得x1=-2,x2=8
x+4=0,解得x1=-2,x2=8
∴C(8,0);
(2)∵抛物线C2与C1恰好关于原点对称,
∴抛物线C2的解析式为y=![]() x2+
x2+![]() x-4,
x-4,
解方程组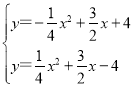 得:
得: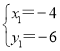 ,
,![]() ,
,
∵点D在第一象限内,
∴D(4,6);
(3)存在.
过B作BN∥y轴,过M作MN∥x轴与BN交于点N,
∵抛物线C2的解析式为y=![]() x2+
x2+![]() x-4=
x-4=![]() (x+3)2-
(x+3)2-![]() ,
,
∴顶点M(-3,-![]() ),
),
∴BN=![]() ,MN=1,
,MN=1,
抛物线C1的对称轴为:直线x=3,设P(3,m)
①以点M,Q,P,B为顶点的四边形为平行四边形,若MQ为对角线,则BM∥PQ,BM=PQ
∴Q(4,m+![]() ),
),
又∵Q为直线y=2x+4上一点,
∴m+![]() =2×4+4,解得:m=
=2×4+4,解得:m=![]()
∴P(3,![]() );
);
②若BM为对角线,设P(3,m),Q(n,2n+4),
∵BM中点坐标为(-![]() ,
,![]() )
)
∴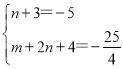 ,解得
,解得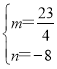 ,
,
∴P(3,![]() ),
),
③若BQ为对角线,∵BM∥PQ,BM=PQ,∴Q(2,8),设P(3,m),
则m-![]() =8+0,解得:m=
=8+0,解得:m=![]() ,
,
∴P(3,![]() )
)
综上所述,存在以点M,Q![]() )或P(3,
)或P(3,![]() ).
).


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
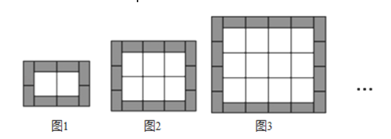
【题目】如图,中间用相同的白色正方形瓷砖,四周用相同的黑色长方形瓷砖铺设矩形地面,请观察图形并解答下列问题.
(1)问:依据规律在第6个图中,黑色瓷砖多少块,白色瓷砖有多少块;
(2)某新学校教室要装修,每间教室面积为68m2 , 准备定制边长为0.5米的正方形白色瓷砖和长为0.5米、宽为0.25米的长方形黑色瓷砖来铺地面.按照此图案方式进行装修,瓷砖无须切割,恰好完成铺设.已知白色瓷砖每块20元,黑色瓷砖每块10元,请问每间教室瓷砖共需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(x1,y1),B(x2,y2)是二次函数上y=ax2-2ax+a-c(a≠0)的两点,若x1≠x2,且y1=y2,则当 自变量x的值取x1+x2时,函数值为( )
A. -cB. cC. -a+cD. a-c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨老师为了了解所教班级学生课后复习的具体情况,对本班部分学生进行了一个月的跟踪调查,然后将调查结果分成四类:A:优秀;B:良好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图.
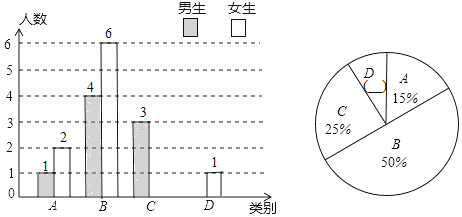
请根据统计图解答下列问题:
(1)本次调查中,杨老师一共调查了 名学生,其中C类女生有 名,D类男生有 名;
(2)补全上面的条形统计图和扇形统计图;
(3)在此次调查中,小平属于D类.为了进步,她请杨老师从被调查的A类学生中随机选取一位同学,和她进行“一帮一”的课后互助学习.请求出所选的同学恰好是一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
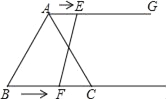
【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=______s时,以A、C、E、F为顶点四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,边AB、BC的长(AB<BC)是方程x2﹣7x+12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).
(1)求AB与BC的长;
(2)当点P运动到边BC上时,试求出使AP长为![]() 时运动时间t的值;
时运动时间t的值;
(3)当点P运动到边AC上时,是否存在点P,使△CDP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax+bx+c与x轴的两个交点为B(1,0)和C,与y轴的交点坐标为(0,-1.5)且此抛物线过点A(3,6).

(1)求此二次函数的解析式;
(2)设此抛物线的顶点为P,对称轴与线段AC相交于点Q,求点P和点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com