
【题目】已知A(x1,y1),B(x2,y2)是二次函数上y=ax2-2ax+a-c(a≠0)的两点,若x1≠x2,且y1=y2,则当 自变量x的值取x1+x2时,函数值为( )
A. -cB. cC. -a+cD. a-c
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析式是![]() ,直线l2的解析式是
,直线l2的解析式是![]() ,点A1在l1上,A1的横坐标为
,点A1在l1上,A1的横坐标为![]() ,作
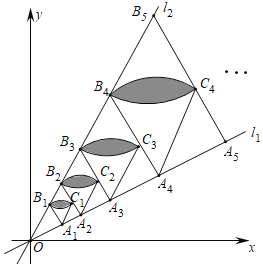
,作![]() 交l2于点B1,点B2在l2上,以B1A1,B1B2为邻边在直线l1,l2间作菱形A1B1B2C1,分别以点A1,B2为圆心,以A1B1为半径画弧得扇形B1A1C1和扇形B1B2C1,记扇形B1A1C1与扇形B1B2C1重叠部分的面积为S1;延长B2C1交l1于点A2,点B3在l2上,以B2A2,B2B3为邻边在l1,l2间作菱形A2B2B3C2,分别以点A2,B3为圆心,以A2B2为半径画弧得扇形B2A2C2和扇形B2B3C2,记扇形B2A2C2与扇形B2B3C2重叠部分的面积为S2……按照此规律继续作下去,则
交l2于点B1,点B2在l2上,以B1A1,B1B2为邻边在直线l1,l2间作菱形A1B1B2C1,分别以点A1,B2为圆心,以A1B1为半径画弧得扇形B1A1C1和扇形B1B2C1,记扇形B1A1C1与扇形B1B2C1重叠部分的面积为S1;延长B2C1交l1于点A2,点B3在l2上,以B2A2,B2B3为邻边在l1,l2间作菱形A2B2B3C2,分别以点A2,B3为圆心,以A2B2为半径画弧得扇形B2A2C2和扇形B2B3C2,记扇形B2A2C2与扇形B2B3C2重叠部分的面积为S2……按照此规律继续作下去,则![]() ________.(用含有正整数n的式子表示)
________.(用含有正整数n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
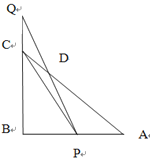
【题目】如图,等腰Rt△ABC的直角边AB=2,点P、Q分别从A、C两点同时出发,以相等的速度作直线运动,已知点P沿射线AB运动,点Q沿边BC的延长线运动,PQ与直线相交于点D.
(1)设AP的长为x,△PCQ的面积为S,求出S关于x的函数关系式;
(2)当AP的长为何值时,![]() =
=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌相机,原售价每台4000元,经连续两次降价后,现售价每台3240元,已知两次降价的百分率一样。
(1)求每次降价的百分率;
(2)如果按这个百分率再降价一次,求第三次降价后的售价?
查看答案和解析>>
科目:初中数学 来源: 题型:
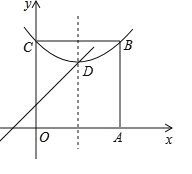
【题目】阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=x+4.如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线![]() 经过B.C两点,顶点D在正方形内部.
经过B.C两点,顶点D在正方形内部.
(1)写出点M(2,3)任意两条特征线___________________
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
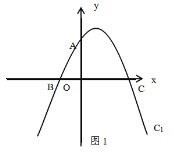
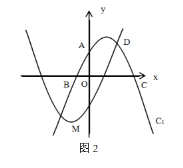
【题目】如图(1),在平面直角坐标系x Oy中,直线y=2x+4与y轴交于点A,与x轴交于点B,抛物线C1:y=![]() x2+bx+c过A,B两点,与x轴的另一交点为点C.
x2+bx+c过A,B两点,与x轴的另一交点为点C.
(1)求抛物线C1的解析式及点C的坐标;
(2)如图(2),作抛物线C2,使得抛物线C2与C1恰好关于原点对称,C2与C1在第一象限内交于点D,连接AD,CD,请直接写出抛物线C2的解析式和点D的坐标.
(3)已知抛物线C2的顶点为M,设P为抛物线C1对称轴上一点,Q为直线y=2x+4上一点,是否存在以点M,Q,P,B为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某单位使用共享单车的情况,该单位有200名员工,某研究小组随机采访10位员工,得到这10位员工一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是
(2)试用平均数估计该单位员工一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4 经过点A(﹣3,0),点 B 在抛物线上,CB∥x轴,且AB 平分∠CAO.则此抛物线的解析式是___________.
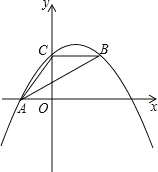
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com