
����Ŀ���Ķ�������Լ��,��ƽ��ֱ������ϵ��,����ij����ƽ�����������ƽ������������н�ƽ���ߵ�ֱ��,�иõ������������.����,��M(1��3)���������У�x=1��y=3��y=x+2��y=x+4.��ͼ,��ƽ��ֱ������ϵ����������OABC,��B�ڵ�һ����,A��C�ֱ���x���y����,������![]() ����B.C���㣬����D���������ڲ�.
����B.C���㣬����D���������ڲ�.
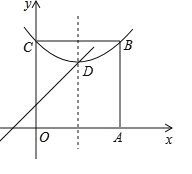
(1)���M��2,3����������������___________________
(2)����D��һ����������y=x+1����������ߵĽ���ʽ________________________
���𰸡�![]()
![]()
��������
��1������������ֱ�������D�������ߣ�
��2���ɵ�D��һ�������ߺ������ε����������D�����꣬�Ӷ���������߽���ʽ��
��1���ߵ�M��2��3����
���M��2��3����x=2��y=3��y=x+1��y=-x+5��
�ʴ�Ϊy=3��y=x+1��(2)��D��һ����������y=x+1����b-a=1����b=a+1
�������߽���ʽΪ![]()
��![]()
���ı���OABC�������Σ���D��Ϊ�����εĶԳ��ᣬD(a��b)��
��B(2a��2b)��
��![]() ����b=a+1����õ�a=2��b=3��
����b=a+1����õ�a=2��b=3��
��D(2��3)��
�������߽���ʽΪ![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��Ϊ��Ȼ���������
��Ϊ��Ȼ���������![]() �ķ���
�ķ���![]() �Ľ�
�Ľ�![]() ���У� ������
���У� ������![]() ��ʾ������ʵ��
��ʾ������ʵ��![]() �����������
�����������
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
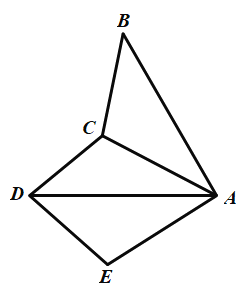
����Ŀ����ͼ������ABC�Ƶ�A��ʱ����ת60���õ���ADE������CD.��![]() ����
����![]() �Ĵ�С��___��
�Ĵ�С��___��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
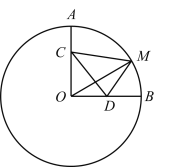
����Ŀ����ͼ���ڡ�O�У���A����B�ڡ�O�ϣ���AOB��90����OA��6����C��OA�ϣ���OC��2AC����D��OB���е㣬��M���ӻ�AB�ϵĶ��㣬��CM+2DM����СֵΪ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���O������ԭ�㣬OA��OC�ֱ���x�ᡢy����������ϣ���OA��5��OC��4��
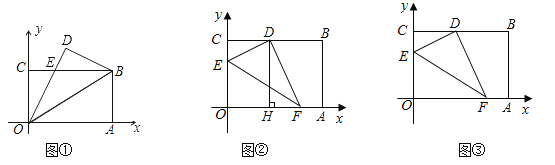
(1)��ͼ�٣��������ضԽ���OB�۵���ʹ�õ�A���ڵ�D����OD��CB�ཻ�ڵ�E�������ص�������OBE��ʲô�����Σ�˵��������ɣ��������������ε������
(2)��ͼ�ڣ���E��F�ֱ���OC��OA���ϵĵ㣬����OEF��EF�۵���ʹ�õ�O��������BC���ϵ�D�㣬����D��DH��OA����EF�ڵ�G����OA�ڵ�H����CD��2�����G�����ꣻ
(3)��ͼ�ۣ���(2)������������E��F��OC��OA���ƶ�ʱ����DҲ�ڱ�BC����֮�ƶ�����ֱ��д��BD��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c��a��0����x�ύ��A����2��0����B��4��0�����㣬��y�ύ�ڵ�C����OC=2OA��
��1�����������ߵĽ���ʽ��
��2��ֱ��y=kx+1��k��0����y�ύ�ڵ�D���������߽��ڵ�P����ֱ��BC���ڵ�M����m=![]() ������m�����ֵ����ʱ��P�����ꣻ
������m�����ֵ����ʱ��P�����ꣻ
��3���ڣ�2���������£���Q��x���ϵ�һ�����㣬��N������ƽ���ڵ�һ�㣬�Ƿ���������ĵ�Q��N��ʹ����P��D��Q��N�ĵ���ɵ��ı����Ǿ��Σ�������ڣ��������N�����ꣻ��������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�����������![]() ��ͼ���
��ͼ���![]() ���ڵ�һ�����ڣ�
���ڵ�һ�����ڣ�![]() ��
��![]() �ᣬ��
�ᣬ��![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��
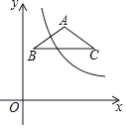
��1��������������![]() ��ͼ����B����˷����������Ľ���ʽ��
��ͼ����B����˷����������Ľ���ʽ��
��2������![]() ����ƽ��
����ƽ��![]() ��m>0������λ���ȣ�
��m>0������λ���ȣ�![]() ��
��![]() ����Ķ�Ӧ��ͬʱ���ڷ���������ͼ���ϣ���
����Ķ�Ӧ��ͬʱ���ڷ���������ͼ���ϣ���![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ƻ�����A��B�������ͽ���̨�ƣ���֪B�ͽ���̨��ÿյ���۱�A�͵Ķ�40Ԫ������3000Ԫ������A�ͽ���̨������5000Ԫ������B�ͽ���̨�Ƶ�������ͬ��
��1����ÿյA�ͽ���̨�ƵĽ����Ƕ���Ԫ��
��2���̳�������A��B���ͽ���̨��100յ�������ۣ�A�ͽ���̨��ÿյ���ۼ�Ϊ90Ԫ��B�ͽ���̨��ÿյ���ۼ�Ϊ140Ԫ����B�ͽ���̨�ƵĽ�������������A�ͽ���̨��������2����Ӧ������������ʹ�̳�������������̨��ʱ����ࣿ��ʱ�����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��x��1�Ƕ��κ���y��ax2+bx+c��a��b��c��ʵ������a��0����ͼ��ĶԳ��ᣬ��A��x1��y1���͵�B��x2��y2��Ϊ��ͼ���ϵ����㣬��y1<y2����������
A.��x1<x2����x1+x2��2��0B.��x1<x2����x1+x2��2>0
C.��x1��x2����a��x1+x2-2����0D.��x1��x2����a��x1+x2-2��<0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com