
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���O������ԭ�㣬OA��OC�ֱ���x�ᡢy����������ϣ���OA��5��OC��4��
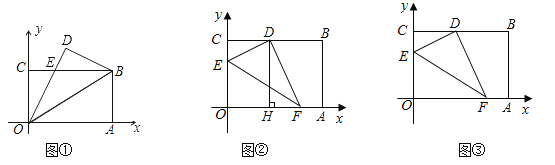
(1)��ͼ�٣��������ضԽ���OB�۵���ʹ�õ�A���ڵ�D����OD��CB�ཻ�ڵ�E�������ص�������OBE��ʲô�����Σ�˵��������ɣ��������������ε������
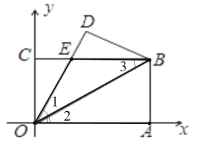
(2)��ͼ�ڣ���E��F�ֱ���OC��OA���ϵĵ㣬����OEF��EF�۵���ʹ�õ�O��������BC���ϵ�D�㣬����D��DH��OA����EF�ڵ�G����OA�ڵ�H����CD��2�����G�����ꣻ
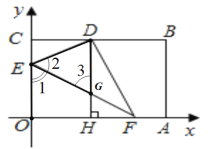
(3)��ͼ�ۣ���(2)������������E��F��OC��OA���ƶ�ʱ����DҲ�ڱ�BC����֮�ƶ�����ֱ��д��BD��ȡֵ��Χ��
���𰸡���1��![]() �ǵ��������Σ����ɼ�������
�ǵ��������Σ����ɼ�������![]() ����2��
����2��![]() ����3��1��BD��3
����3��1��BD��3
��������
��1�������۵������ʺ;��ε����ʣ��ó�![]() ��
��![]() �������õ�
�������õ�![]() �ǵ��������Σ������ù��ɶ������EB�ij���������������ɣ�
�ǵ��������Σ������ù��ɶ������EB�ij���������������ɣ�
��2���õ�G�ĺ�����Ϊ2�������۵������ʺ�DH��OA���ó�![]() ������
������![]() �����ù��ɶ������DG�ij����ɵõ���G�������ꣻ
�����ù��ɶ������DG�ij����ɵõ���G�������ꣻ
��3��������������ǣ��ٵ���E�˶������C�غ�ʱ���ڵ���F�˶������A�غ�ʱ���ֱ����BD��ֵ�����ɵõ�BD��ȡֵ��Χ��
��1��![]() �ǵ��������Σ��������£�
�ǵ��������Σ��������£�
����ͼ��
![]() ͼ���۵�
ͼ���۵�
![]()
![]() ����
����![]()
![]()
��![]()
![]()
![]()
![]() �ǵ���������
�ǵ���������
��![]() ����
����![]()
��![]() ��
�У�![]()
���![]()
![]()
��2������ͼ��
��ͼ���۵�
![]()
![]()
![]()
![]()
![]()
![]() ��
��![]() �ǵ���������
�ǵ���������
��![]() ����
����![]()
��![]() ��
��
![]() �����
�����![]()
![]()
��![]()
��3���ٵ���E�˶������C�غ�ʱ������ͼ��
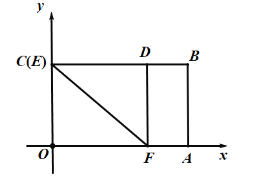
��ʱ��CD=OC=4����BD=BC-CD=1��
�ڵ���F�˶������A�غ�ʱ������ͼ��
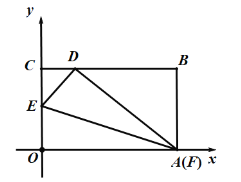
��ʱ��AD=OA=5����Rt��ABD�У�BD=![]() =
=![]() =3��
=3��
��BD��ȡֵ��ΧΪ1��BD��3.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ഺ��֧���ھ���ƶ��У���������ƶ����ͥ���ͼס������������������֣���֪��������ļ۸�ȼ��������10Ԫ����480Ԫ������������Ŀ���ǡ������360Ԫ�����������Ŀ�����ͬ��
��1����ס�����������ÿ�õļ۸���Ƕ���Ԫ��
��2����ʵ�ʰ���У����Ǿ����ٴι���ס����������繲50�ã���ʱ������������ۼ۱ȵ�һ�ι���ʱ������10%������������ۼ۲��䣬����ٴι�������������ܷ��ò�����1500Ԫ����ô�������ɹ�����ٿ��������磿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ��ŷ���dz��Ƴ�۲���������˵����������֪�������������ʣ�����ͨ���۲췢�ֵģ���ʷ�������ң�������ŵĹ۲�ң�������ǽ����ٵ�������ת��Ϊ�Ѿ���Ϥ�Ĺ淶�������ѧ����������һ�־����ձ������Ե���ѧ˼�뷽���������ʽ���Զ���ʽ��������ڶ�λ���ij������м��㣺
�������Ϸ�������������⣺
��1�����㣺��x3+2x2��3x��10������x��2����
��2��������x�Ķ���ʽ2x4+5x3+ax2+b�ܱ�����ʽx+2��������a��b��Ϊ��Ȼ��������������������a��b��ֵ����Ӧ���̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����κ���y=x2+2x+3��һ�κ���y=3x+5��
��1����������ͼ���ཻ�����ཻ���м������㣿
��2����ֱ��y=3x+5����ƽ��k����λ��ʹֱ����������ֻ��һ�����㣬��k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������ǿ��ë������ƹ���������������������˶���ÿλͬѧ������ֻ��ѡ��һ�������˶����Ը�Уѧ�������ȡ![]() ���е��飬���ݵ��������������²�������Ƶ���ֲ���������ͳ��ͼ��
���е��飬���ݵ��������������²�������Ƶ���ֲ���������ͳ��ͼ��
�˶���Ŀ | Ƶ��(����) |
��� | 30 |
���� |
|
ƹ���� | 36 |
���� |
|
���� | 12 |

����������ͼ����Ϣ����������⣺
(1)Ƶ���ֲ����е�![]() ��
��![]() ��
��
(2)������ͳ��ͼ�У����������ڵ����ε�Բ�Ľ�Ϊ ����
(3)ȫУ�ж�����ѧ��ѡ��μ�ƹ�����˶���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������Լ��,��ƽ��ֱ������ϵ��,����ij����ƽ�����������ƽ������������н�ƽ���ߵ�ֱ��,�иõ������������.����,��M(1��3)���������У�x=1��y=3��y=x+2��y=x+4.��ͼ,��ƽ��ֱ������ϵ����������OABC,��B�ڵ�һ����,A��C�ֱ���x���y����,������![]() ����B.C���㣬����D���������ڲ�.
����B.C���㣬����D���������ڲ�.
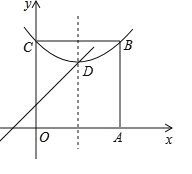
(1)���M��2,3����������������___________________
(2)����D��һ����������y=x+1����������ߵĽ���ʽ________________________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽƬABCD�У���E��AD���е㣬��AE��1������BE���ֱ���B��EΪԲ�ģ��Դ���![]() �ij�Ϊ�뾶�������������ڵ�M��N����ֱ��MNǡ�ù���C����AB�ij���Ϊ��������
�ij�Ϊ�뾶�������������ڵ�M��N����ֱ��MNǡ�ù���C����AB�ij���Ϊ��������
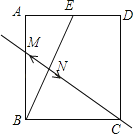
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�дӲ�ͬѧУ�����ȡ100������������ʹ����ѧ�̸�����IJ��������е��飬ͳ�ƽ�����£�
���� | 0 | 1 | 2 | 3 |
���� | 10 | 20 | 30 | 40 |
�����������ݣ�����˵����ȷ���ǣ�������
A.������2��B.�����2��
C.ƽ������3��D.������1.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У��ȫ��Խ��Խ�ܵ����ǵĹ�ע������ij��ѧ�Բ���ѧ����У��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ������ͼ����Ϣ�ش��������⣺

��1�������ʾ������ѧ������______�ˣ�����ͳ��ͼ��m��ֵΪ______��
��2������ͳ��ͼ�����˽��������������Ӧ���ε�Բ�ĽǵĶ���Ϊ______��
��3��������ѧ����ѧ��1800�ˣ��������������������Թ��Ƴ���ѧУѧ���ж�У��ȫ֪ʶ�ﵽ���dz��˽������������˽����̶ȵ�������Ϊ______�ˣ�
��4�����Ӷ�У��ȫ֪ʶ�ﵽ���dz��˽����̶ȵ�2��������2��Ů���������ȡ2�˲μ�У��ȫ֪ʶ�����������б�����״ͼ�ķ�������ǡ�ó鵽1��������1��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com