
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点P从点A开始沿着
,若动点P从点A开始沿着![]() 的路径运动,且速度为每秒2cm,设点P运动的时间为t秒.
的路径运动,且速度为每秒2cm,设点P运动的时间为t秒.
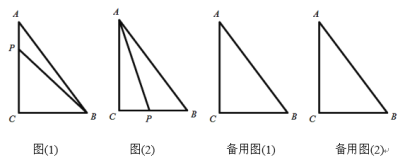
(1)当![]() 时,
时,![]() 的面积是___________
的面积是___________![]() ;
;
(2)如图(2)当t为何值时,AP平分![]() ;
;
(3)当t为何值时,![]() 为等腰三角形.
为等腰三角形.
【答案】(1)45;(2)![]() ;(3)t=2.5秒或25或26.5或23.75.
;(3)t=2.5秒或25或26.5或23.75.
【解析】
(1)当t=3时,求出AP的长,再根据三角形面积公式即可得出结果;
(2)作PD⊥AB于D,由勾股定理求出AB的长,由角平分线性质得出PD=PC=2t-20(cm),AD=AC=20cm,求出BD的长,得出PB=BC-PC=35-2t(cm),在Rt△PBD中,由勾股定理求出t的值即可;
(3)由于点P是动点,故应分点P在AC上与AB上两种情况进行讨论,根据等腰三角形的性质和相似三角形的判定与性质即可得出结果.
(1)当t=3时,AP=2×3=6(cm),
△ABP的面积=![]() AP×BC=
AP×BC=![]() ×6×15=45(cm2);
×6×15=45(cm2);
故答案为:45cm2;
(2)作PD⊥AB于D,如图2所示:
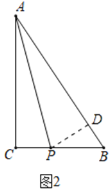
∵在△ABC中,∠C=90°,AC=20cm,BC=15cm,
∴AB=![]() (cm),
(cm),
∵AP平分∠CAB,
∴PD=PC=2t-20(cm),AD=AC=20cm,
∴BD=AB-AD=5cm,
∴PB=BC-PC=15-(2t-20)=35-2t(cm),
在Rt△PBD中,由勾股定理得:BD2+PD2=PB2,
即52+(2t-20)2=(35-2t)2,
解得:t=![]() ,
,
∴当t为![]() 时,AP平分∠CAB;
时,AP平分∠CAB;
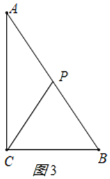
(3)当点P在AC上时,CP=CB=15cm,
∴AP=AC-CP=5cm,
∴t=2.5秒;
当点P在AB上时,分三种情况:
若BP=BC=15cm,t=(20+15+15)÷2=25(秒);
若CP=BC=15cm,
作CM⊥AB,则BM=PM,
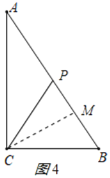
∵∠B=∠B,∠BMC=∠BCA,
∴△ABC∽△CBM,
∴![]() ,即
,即![]() ,
,
解得:CM=12cm,BM=9cm,
∴PB=2BM=18cm,
∴t=(20+15+18)÷2=26.5(秒);
若PC=PB,则∠B=∠BCP,
∵∠B+∠A=90°,∠BCP+∠ACP=90°,
∴∠A=∠ACP,
∴AP=CP=BP=![]() AB=12.5cm,
AB=12.5cm,
∴t=(20+15+12.5)÷2=23.75(秒);
综上所述,当t=2.5秒或25或26.5或23.75秒时,△BCP为等腰三角形.


科目:初中数学 来源: 题型:
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) |
|
|
售价(元/件) | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共50件,其中销售甲种商品为![]() 件(
件(![]() ),设销售完50件甲、乙两种商品的总利润为
),设销售完50件甲、乙两种商品的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个三角形的一个内角等于另一个内角的两倍,则称这样的三角形为“倍角三角形”.
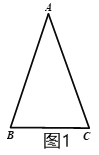
(1)如图1,△ABC中,AB=AC,∠A为36°,求证:△ABC 是锐角三角形;
(2)若△ABC是倍角三角形,![]() ,∠B=30°,AC=
,∠B=30°,AC=![]() ,求△ABC面积;
,求△ABC面积;
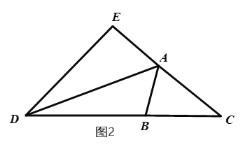
(3)如图2,△ABC的外角平分线AD与CB的延长线相交于点D,延长CA到点E,使得AE=AB,若AB+AC=BD,请你找出图中的倍角三角形,并进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①![]() =﹣1;②ac+b+1=0;③abc>0;④a﹣b+c>0.其中正确的个数是( )
=﹣1;②ac+b+1=0;③abc>0;④a﹣b+c>0.其中正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
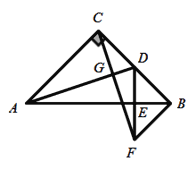
【题目】如图,在等腰![]() 中,
中,![]() ,D为BC的中点,过点C作
,D为BC的中点,过点C作![]() 于点G,过点B作
于点G,过点B作![]() 于点B,交CG的延长线于点F,连接DF交AB于点E.
于点B,交CG的延长线于点F,连接DF交AB于点E.
(1)求证:![]() ;
;
(2)求证:AB垂直平分DF;
(3)连接AF,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
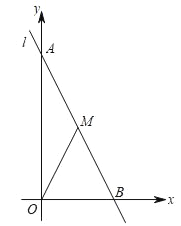
【题目】如图,已知在平面直角坐标中,直线l:y=﹣2x+6分别交两坐标于A、B两点,M是级段AB上一个动点,设点M的横坐标为x,△OMB的面积为S.
(1)写出S与x的函数关系式;
(2)当△OMB的面积是△OAB面积的![]() 时,求点M的坐标;
时,求点M的坐标;
(3)当△OMB是以OB为底的等腰三角形,求它的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com