
【题目】已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题:
(1)请用t分别表示A、B的路程sA、sB;
(2)在A出发后几小时,两人相距15km?

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源: 题型:
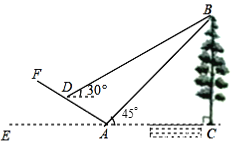
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1︰2.则小明从点A走到点D的过程中,他上升的高度为____米;大树BC的高度为____米(结果保留根号).
米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1︰2.则小明从点A走到点D的过程中,他上升的高度为____米;大树BC的高度为____米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P1(﹣1,y1),P2(2,y2),P3(5,y3)均在二次函数y=﹣x2+2x+c的图象上,则y1,y2,y3的大小关系是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=10,C、D为⊙O上不同于A、B的两点,OC平分∠ACD,连结BC,BD.
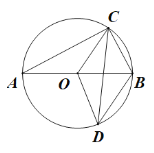
(1)求证:OC∥BD;
(2)过点C作CE⊥DB,垂足为点E.
①求证:△CBE∽△DCE;②若AC=8,求BD的长;
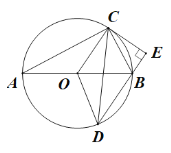
(3)直接写出△BCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2![]() ,Q为AC上的动点,P为Rt△ABC内一动点,且满足∠APB=120°,若D为BC的中点,则PQ+DQ的最小值是( )
,Q为AC上的动点,P为Rt△ABC内一动点,且满足∠APB=120°,若D为BC的中点,则PQ+DQ的最小值是( )

A. ![]() B.
B. ![]() C. 4D.
C. 4D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:经过三角形一边中点,且平分三角形周长的直线叫做这个三角形在该边上的中分线,其中落在三角形内部的部分叫做中分线段.
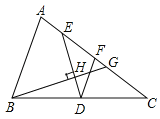
(1)如图,△ABC中,AC>AB,DE是△ABC在BC边上的中分线段,F为AC中点,过点B作DE的垂线交AC于点G,垂足为H,设AC=b,AB=c.
①求证:DF=EF;
②若b=6,c=4,求CG的长度;
(2)若题(1)中,S△BDH=S△EGH,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象经过点(2,-5),顶点坐标为(-1,4),直线l的解析式为y=2x+m.
(1)求抛物线的解析式;
(2)若抛物线与直线l有两个公共点,求![]() 的取值范围;
的取值范围;
(3)若直线l与抛物线只有一个公共点P,求点P的坐标;
(4)设抛物线与![]() 轴的交点分别为A、B,求在(3)的条件下△PAB的面积.
轴的交点分别为A、B,求在(3)的条件下△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,AB⊥AD,AB⊥BC,以AB为直径的⊙O与CD相切于点E,连接OC、OD.
(1)求证:OC⊥OD;
(2)如图2,连接AC交OE于点M,若AB=4,BC=1,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com