
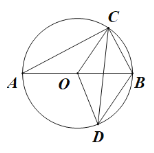
【题目】如图,⊙O的直径AB=10,C、D为⊙O上不同于A、B的两点,OC平分∠ACD,连结BC,BD.
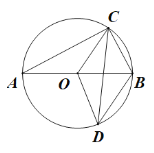
(1)求证:OC∥BD;
(2)过点C作CE⊥DB,垂足为点E.
①求证:△CBE∽△DCE;②若AC=8,求BD的长;
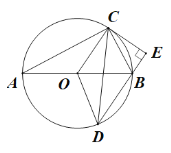
(3)直接写出△BCD面积的最大值.
【答案】(1)见解析;(2)①见解析;②BD=2.8;(3)△BCD面积的最大值为![]()
【解析】
(1)根据同弧所对的圆周角相等得∠BDC=∠BAC,再由半径相等和角平分线定义等量代换得∠OCD=∠CDB即可证明;
(2)①根据(1)的结论和CE⊥DB可得CE⊥OC,进而得∠ECB=∠CDB,即可证明两三角形相似;②根据勾股定理先求BC的长,再证明△ABC和△CBE相似,对应边成比例可求出CE和BE的长,由①中的三角形相似对应边成比例求出DE的长进而求得BD的长;
(3)根据(2)的过程即可表示△BCD的最大面积;
(1)∵∠BDC和∠BAC是同弧所对的圆周角,
∴∠BDC=∠BAC,
∴OA=OC,
∴∠OAC=∠OCA,
∵OC平分∠ACD,
∴∠OCA=∠OCD,
∴∠OCD=∠CDB,
∴OC∥BD;
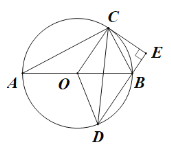
(2)①证明:∵OC∥BD,CE⊥DE,
∴CE⊥OC,
∴∠CEB=90°,
∴∠ECB+∠OCB=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠ACO+∠OCB=90°,
∴∠ACO+∠OCB=90°,
∴∠ECB=∠ACO,
∵∠ACO=∠CDB,
∴∠ECB=∠CDB,∠CEB=∠DEC,
即△CBE![]() △DCE;
△DCE;
②由①得,∠ACO=∠ECB,∠ACB=∠BEC=90°,
∴△ABC![]() △CBE,
△CBE,
∴![]() ,
,
∵Rt△ABC中,AB=10,AC=8,根据勾股定理得,BC=6,
∴![]() ,
,
解得![]() ,
,![]() ,
,
由①得,△CBE![]() △DCE,
△DCE,
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴BD=DE-BE=![]() =2.8;
=2.8;
(3)如图:过点O作OG⊥BD于点G,
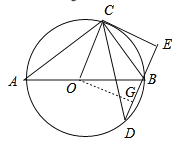
由(2)CE⊥BD,OC⊥CE,
可得四边形COGE是矩形,
∴OC=GE=5,CE=OG,
设BG=x,则BD=2x,BO=5,
在Rt△BGO中,根据勾股定理,得,
![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
∴![]() 的最大值为为
的最大值为为![]()
∴S的最大值为为![]() ;
;
即△BCD面积的最大值为为![]() ;
;


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚根据以往的学习经验,想通过由“特殊到一般”的方法探究下面二次根式的运算规律.
以下是小刚的探究过程,请补充完整.
(1)具体运算,发现规律:
特例1:![]() ;特例2:
;特例2:![]() ;特例3:
;特例3:![]() ;
;
特例4:______(举一个符合上述运算特征的例子);
(2)观察、归纳,得出猜想:
如果![]() 为正整数,用含
为正整数,用含![]() 的式子表示这个运算规律:______;
的式子表示这个运算规律:______;
(3)请你证明猜想的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦放假期间,小明和小华准备到西安的大雁塔(记为A)、白鹿原(记为B)、兴庆公园(记为C)、秦岭国家植物园(记为D)中的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点被选中的可能性相同.
(1)求小明选择去白鹿原游玩的概率;
(2)用树状图或列表的方法求小明和小华都选择去秦岭国家植物园游玩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里有1个红球和n个白球,它们除颜色外其余都相同.
(1)从这个袋子里摸出一个球,记录其颜色,然后放回,摇均匀后,重复该实验,经过大量实验后,发现摸到白球的频率稳定于![]() 左右,求n的值;
左右,求n的值;
(2)在(1)的条件下,先从这个袋中摸出一个球,记录其颜色,放回,摇均匀后,再从袋中摸出一个球,记录其颜色.请用画树状图或者列表的方法,求出先后两次摸出不同颜色的两个球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题:
(1)请用t分别表示A、B的路程sA、sB;
(2)在A出发后几小时,两人相距15km?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若1表示的点与﹣1表示的点重合,则﹣3表示的点与数 表示的点重合;
(2)若﹣1表示的点与3表示的点重合,回答以下问题:
①原点与数 表示的点重合;
②若数轴上A、B两点之间的距离为7,且A、B两点经折叠后重合,则A、B两点表示的数是
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
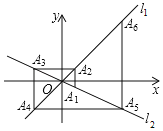
【题目】如图,在平面直角坐标系中,函数y=x和![]() 的图象分别为直线l1、l2,过点A1(1,
的图象分别为直线l1、l2,过点A1(1,![]() )作x轴的垂线交l1于点A2,过点A2作y轴的垂线交l2于点A3,过点A3作x轴的垂线交l1于点A4,过点A4作y轴的垂线交l2于点A5,……依次进行下去,则点A2019的横坐标为( )
)作x轴的垂线交l1于点A2,过点A2作y轴的垂线交l2于点A3,过点A3作x轴的垂线交l1于点A4,过点A4作y轴的垂线交l2于点A5,……依次进行下去,则点A2019的横坐标为( )
A.21008B.﹣21008C.﹣21009D.21006
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com