
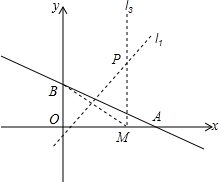
 ��ͼ��ֱ��y=kx+3��x�ᡢy��ֱ���A��B���㣬tan��OAB=$\frac{3}{4}$����M��x���ϵ�һ�����㣮����BM�����߶�BN�Ĵ�ֱƽ����l1������M��x�ᴹ��l2 ��l1��l2�Ľ���ΪP��
��ͼ��ֱ��y=kx+3��x�ᡢy��ֱ���A��B���㣬tan��OAB=$\frac{3}{4}$����M��x���ϵ�һ�����㣮����BM�����߶�BN�Ĵ�ֱƽ����l1������M��x�ᴹ��l2 ��l1��l2�Ľ���ΪP������ ��1����������ֵ���ɵ�A�����꣬���ݴ���ϵ�������ɵú�������ʽ��
��2�����ݴ���ϵ�������ɵ�BM�Ľ���ʽ�������߶δ�ֱƽ���ߵ����ʣ��ɵ�PC�Ľ���ʽ�������Ա�����ֵ���ɵú�����ϵʽ��
��3�����ݹ��ɶ�������ȫƽ����ʽ���ɵô𰸣�
��4�����ݵȱ������ε����ʣ��ɵ�B��E�����������ȣ����ݽⷽ�̣��ɵ�xֵ������P������꣬�ɵô𰸣�
��� �⣺��1����ֱ��y=kx+3��y��ֱ���B�㣬
��B��0��3����
��tan��OAB=$\frac{3}{4}$��
��OA=4��
��A��4��0����
��ֱ��y=kx+3��A��4��0����
��4k+3=0��
��k=-$\frac{3}{4}$��
��ֱ�ߵĽ���ʽΪ��y=-$\frac{3}{4}$x+3��
��2����M��������a��0����
BM�е�C������Ϊ��$\frac{a}{2}$��$\frac{3}{2}$��
BM�Ľ���ʽΪy=-$\frac{3}{a}$x+3��
��PC�ĺ�������ʽΪy=$\frac{a}{3}$x+b��
��C��������룬��
b=$\frac{3}{2}$-$\frac{{a}^{2}}{6}$��
PC�ĺ�������ʽΪy=$\frac{a}{3}$x+$\frac{3}{2}$-$\frac{{a}^{2}}{6}$��
��x=a�裬y=$\frac{1}{6}$a2+$\frac{3}{2}$��
P��ĺ�������ʽΪy=$\frac{1}{6}$x2+$\frac{3}{2}$��
��3��PB��С=$\sqrt{{x}^{2}+��\frac{1}{6}{x}^{2}+\frac{3}{2}-3��^{2}}$=$\sqrt{��\frac{1}{6}{x}^{2}+\frac{3}{2}��^{2}}$=$\frac{3}{2}$��
��4�����ڵ�P��ʹ��PBMΪ�ȱ������Σ��������£�
BE��MP��BE��x�ᣬ
$\frac{1}{6}$x2+$\frac{3}{2}$=6��
���x1=3$\sqrt{3}$��x2=-3$\sqrt{3}$��
P1��3$\sqrt{3}$��6����P2��-3$\sqrt{3}$��6����
���� ���⿼����һ�κ����ۺ��⣬���ô���ϵ������������ʽ���߶δ�ֱƽ���ߵĹ�ϵ���ȱ������ε����ʣ������߶δ�ֱƽ���ߵó�PC�Ľ���ʽ�ǽ⣨2���Ĺؼ������õȱ������ε������ǽ⣨3���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
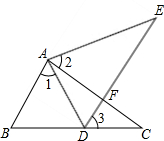 ��ͼ����E�ڡ�ABC�ⲿ����D��BC���ϣ�DE��AC�ڵ�F������1=��2=��3��AC=AE�����ҳ�ͼ�е�ȫ�������Σ�������֤����
��ͼ����E�ڡ�ABC�ⲿ����D��BC���ϣ�DE��AC�ڵ�F������1=��2=��3��AC=AE�����ҳ�ͼ�е�ȫ�������Σ�������֤�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
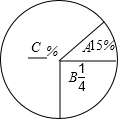 ��ͼ��Բ�ֳ�A��B��C���������Σ��Ұ뾶Ϊ3cm��
��ͼ��Բ�ֳ�A��B��C���������Σ��Ұ뾶Ϊ3cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4cm | B�� | $4\sqrt{2}$cm | C�� | $4\sqrt{3}$cm | D�� | 6cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �½��߶�d���ף� | 20 | 80 | 245 | 320 |
| �½�ʱ��t���룩 | 2 | 4 | 7 | 8 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com