
分析 分子变为(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{99}$+$\frac{1}{100}$)-2×($\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{100}$),然后通过计算,变为与分母相同,解解决问题.
解答 解:$\frac{1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{99}-\frac{1}{100}}{\frac{1}{101^2-1^2}+\frac{1}{102^2-2^2}+…+\frac{1}{150^2-50^2}}$
=$\frac{(1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{99}+\frac{1}{100})-2×(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{100})}{\frac{1}{200}(\frac{1}{51}+\frac{1}{52}+…+\frac{1}{100})}$
=$\frac{200(1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{99}+\frac{1}{100}-1-\frac{1}{2}-\frac{1}{3}-…-\frac{1}{50})}{\frac{1}{51}+\frac{1}{52}+…+\frac{1}{100}}$
=200.
故答案为:200.
点评 考查了有理数的混合运算,本题难度较大,关键是将分子变为(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{99}$+$\frac{1}{100}$)-2×($\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{100}$).


科目:初中数学 来源: 题型:选择题
| A. | $±\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $-\frac{1}{3}$ | D. | $±\frac{1}{81}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
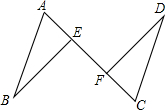 如图,线段AB∥CD,AB=CD=$\sqrt{10}$,连接AC,E、F是AC上的两点,且BE∥DF.
如图,线段AB∥CD,AB=CD=$\sqrt{10}$,连接AC,E、F是AC上的两点,且BE∥DF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三个数中一定有一个是0 | |
| B. | 三个数若都不为0,则不可能符号都相间 | |
| C. | 一定有两个数互为相反数 | |
| D. | 一定有两个数的和等于第三个数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
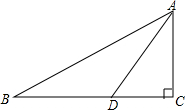 已知:如图,在Rt△ABC中,∠C=90°,点D在边BC上,且$\frac{AB}{DA}$=$\frac{BC}{AC}$.求证:∠B=∠DAC.
已知:如图,在Rt△ABC中,∠C=90°,点D在边BC上,且$\frac{AB}{DA}$=$\frac{BC}{AC}$.求证:∠B=∠DAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
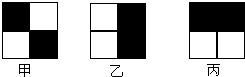
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 三个都一样 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com