
分析 (1)先算乘除,然后算加减即可;
(2)先算乘方,再运用乘法的分配律计算即可;
(3)按照有理数混合运算的顺序,先乘方后乘除最后算加减,有括号的先算括号里面的.
解答 解:(1)$27×(-\frac{2}{3})÷3-(-8)÷4$
=-18÷3+2
=-6+2
=-4;
(2)$(-\frac{1}{2}+\frac{3}{4}-\frac{7}{8})×{(-2)^2}$
=(-$\frac{1}{2}$+$\frac{3}{4}$-$\frac{7}{8}$)×4
=-2+3-$\frac{7}{2}$
=-$\frac{5}{2}$;
(3)$-{5^2}×|{1-\frac{7}{5}}|+\frac{3}{2}×[{{{(-1)}^3}-5}]$
=-25×$\frac{2}{5}$+$\frac{3}{2}$×(-6)
=-10-9
=-19.
点评 本题考查的是有理数的运算能力.注意:
(1)要正确掌握运算顺序,在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序;
(2)去括号法则:--得+,-+得-,++得+,+-得-.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
 阅读理解
阅读理解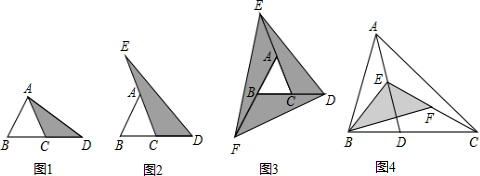
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个数的绝对值等于它本身,则这个数一定是正数 | |
| B. | 没有最小的有理数,也没有绝对值最小的有理数 | |
| C. | 有理数的绝对值一定是正数 | |
| D. | 如果$\frac{|a|}{a}=-1$,那么a<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x2-x+1的一次项系数是1 | B. | xyz的系数是0 | ||
| C. | a2b3c是五次单项式 | D. | x5+3x2y4-2x3y是六次三项式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com