
 شؤ¶ءہي½â
شؤ¶ءہي½â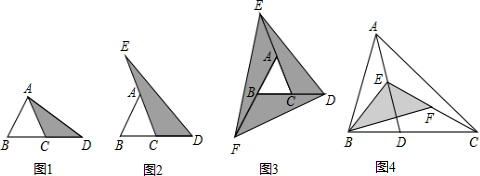
·ضخِ £¨1£©سة،÷ABCسë،÷ACDضذBC=CD£¬سةب½اذخضذدكµب·ضب½اذخµؤأو»¼´؟ة½ل¹û£»
£¨2£©ء¬½سAD£¬سةCD=BC£¬سةب½اذخضذدكµب·ضب½اذخµؤأو»£¬ح¬ہي؟ةµأ،÷AEDسë،÷ADCأو»دàµب£¬¶ّ،÷CDEأو»µبسعء½ب½اذخأو»ض®؛ح£¬¼´؟ةµأ³ِ½ل¹û£»
£¨3£©ء¬½سAD£¬EB£¬FC£¬¸ù¾فµع¶ختµؤث¼آ·£¬ح¬ہي؟ةµأزُس°²؟·ضµؤأو»µبسع6±¶µؤ،÷ABCأو»£¬¼´؟ةµأ³ِ½ل¹û£»
حطص¹س¦سأ£؛µمEتادك¶خADµؤضذµم£¬سةب½اذخضذدكµب·ضب½اذخµؤأو»£¬اَµأS،÷BCE=$\frac{1}{2}$S،÷ABC£¬سةµمFتادك¶خCEµؤضذµم£¬¸ù¾فب½اذخضذدكµب·ضب½اذخµؤأو»£¬اَµأS،÷BEF=S،÷BCF=$\frac{1}{2}$S،÷BCE£¬¼´؟ةاَ³ِ،÷BEFµؤأو»£®
½â´ً ½â£؛£¨1£©،كBC=CD£¬ب½اذخضذدكµب·ضب½اذخµؤأو»£¬
،àS،÷ABC=S،÷ACD£»
¹ت´ً°¸خھ£؛S،÷ABC=S،÷ACD£»
£¨2£©ء¬½سAD£¬بçح¼1ثùت¾£؛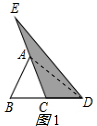 ،كBC=CD£¬ب½اذخضذدكµب·ضب½اذخµؤأو»£¬
،كBC=CD£¬ب½اذخضذدكµب·ضب½اذخµؤأو»£¬
،àS،÷ABC=S،÷ADC£¬
ح¬ہيS،÷ADE=S،÷ADC£¬
،àS،÷CDE=2S،÷ABC£»
¹ت´ً°¸خھ£؛S،÷CDE=2S،÷ABC£»
£¨3£©ء¬½سAD£¬EB£¬FC£¬بçح¼2ثùت¾£؛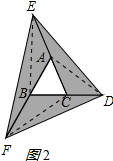
سة£¨2£©µأ£؛S،÷CDE=2S،÷ABC£¬
ح¬ہي؟ةµأ£؛S،÷AEF=2S،÷ABC£¬S،÷BFD=2S،÷ABC£¬
،àS،÷EFD=S،÷CDE+S،÷AEF+S،÷BFD+S،÷ABC=2S،÷ABC+2S،÷ABC+2S،÷ABC+S،÷ABC=7S،÷ABC£»
¹ت´ً°¸خھ£؛S،÷EFD=7S،÷ABC£»
حطص¹س¦سأ£؛
،كµمEتادك¶خADµؤضذµم£¬سةب½اذخضذدكµب·ضب½اذخµؤأو»£¬
،àS،÷ABE=S،÷BDE£¬S،÷ACE=S،÷CDE£¬
،àS،÷BCE=$\frac{1}{2}$S،÷ABC£¬
،كµمF·ض±ًتادك¶خCEµؤضذµم£¬سةب½اذخضذدكµب·ضب½اذخµؤأو»£¬
،àS،÷BEF=S،÷BCF=$\frac{1}{2}$S،÷BCE£¬
،àS،÷BEF=$\frac{1}{4}$S،÷ABC=$\frac{1}{4}$،ء18=4.5£¨cm2£©£»
¹ت´ً°¸خھ£؛4.5£®
µمئہ ±¾جâتاأو»¼°µب»±ن»»×غ؛دجâؤ؟£¬؟¼²éءثب½اذخµؤأو»¼°µب»±ن»»£¬±¾جâسذز»¶¨ؤر¶ب£¬ذèزھح¨¹×÷¸¨ضْدك£¬شثسأب½اذخضذدكµب·ضب½اذخµؤأو»²إؤـµأ³ِ½ل¹û£®



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛½â´ًجâ
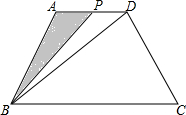 ثؤ±كذخABCDضذ£¬AD،خBC£¬AB=CD=5£¬AD=7£¬BC=13£¬Sثؤ±كذخABCD=40£¬Pتاز»¶¯µم£¬رطAD£¬DCسةA¾DµمدٍCµمزئ¶¯£¬ةèPµمزئ¶¯µؤ¾àہëخھx£®
ثؤ±كذخABCDضذ£¬AD،خBC£¬AB=CD=5£¬AD=7£¬BC=13£¬Sثؤ±كذخABCD=40£¬Pتاز»¶¯µم£¬رطAD£¬DCسةA¾DµمدٍCµمزئ¶¯£¬ةèPµمزئ¶¯µؤ¾àہëخھx£®²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛ر،شٌجâ
| A£® | £¨3£¬5£© | B£® | £¨5£¬-3£© | C£® | £¨-5£¬3£© | D£® | £¨-5£¬-3£© |
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛جî؟صجâ
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛½â´ًجâ
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛½â´ًجâ
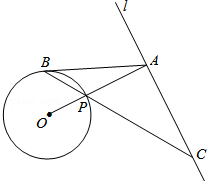 بçح¼£¬زرضھض±دكlسë،رOدàہ룬OA،حlسعµمA£¬½»،رOسعµمP£¬µمBتا،رOةدز»µم£¬ء¬½سBP²¢رس³¤£¬½»ض±دكlسعµمC£¬ت¹µأAB=AC£®
بçح¼£¬زرضھض±دكlسë،رOدàہ룬OA،حlسعµمA£¬½»،رOسعµمP£¬µمBتا،رOةدز»µم£¬ء¬½سBP²¢رس³¤£¬½»ض±دكlسعµمC£¬ت¹µأAB=AC£®²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛ر،شٌجâ
| A£® | 1 | B£® | 3 | C£® | 7 | D£® | 5 |
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛½â´ًجâ
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛½â´ًجâ
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com