
分析 利用反例可对①②③⑥进行判断;根据有理数的性质对④进行判断;利用偶数次方的意义可对⑤进行判断.
解答 解:两数相加,和不一定大于每个加数,如-1与-2相加,所以①错误;
两个数的差不一定小于这两个数的和,如-1与-2的差为1,-1与-2的和为-3,所以②错误;
零减去一个数不一定得负数,如0减去-1得1,所以③错误;
如果两个有理数的商是负数,那么它们的积也是负数,所以④正确;
任何有理数的偶次方都是非负数,所以⑤错误;
任何数的倒数不一定都比它本身小,如-2的倒数为-$\frac{1}{2}$,所以⑥错误.
故答案为④.
点评 本题考查了有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.


科目:初中数学 来源: 题型:解答题
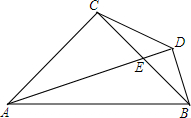 知图,△ACB为等腰直角三角形,∠ACB=90°,AC=BC,AE平分∠BAC,BD⊥AE,垂足为D点.
知图,△ACB为等腰直角三角形,∠ACB=90°,AC=BC,AE平分∠BAC,BD⊥AE,垂足为D点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读理解
阅读理解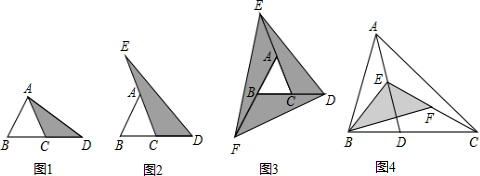
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个数的绝对值等于它本身,则这个数一定是正数 | |
| B. | 没有最小的有理数,也没有绝对值最小的有理数 | |
| C. | 有理数的绝对值一定是正数 | |
| D. | 如果$\frac{|a|}{a}=-1$,那么a<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com