
分析 (1)根据a?b=a×b-a-b,可以得到3?(-5)的值;
(2)根据a?b=a×b-a-b,可以得到4?(-2)与(-2)?4的值,从而可以比较大小;
(3)根据a?b=a×b-a-b,我们可以得到b?a,从而可以解答本题.
解答 解:(1)3?(-5)
=3×(-5)-3-(-5)
=-15-3+5
=-13;
(2)∵4?(-2)
=4×(-2)-4-(-2)
=-8-4+2
=-10,
(-2)?4
=(-2)×4-(-2)-4
=-8+2-4
=-10,
∴4?(-2)=(-2)?4,
故答案为:=;
(3)∵a?b=a×b-a-b,b?a=b×a-b-a
∴a?b=b?a,
∴运算:“?”满足交换律,
即运算:“?”满足交换律,
故答案为:=.
点评 本题考查有理数的混合运算,解题的关键是明确新定义,并且可以根据新定义进行解答问题.


科目:初中数学 来源: 题型:解答题
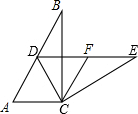 如图,在Rt△ABC中,∠ACB=90°,∠B=α,将△ABC绕点C按顺时针方向旋转β后得到△DEC,点D恰好落在AB边上.
如图,在Rt△ABC中,∠ACB=90°,∠B=α,将△ABC绕点C按顺时针方向旋转β后得到△DEC,点D恰好落在AB边上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
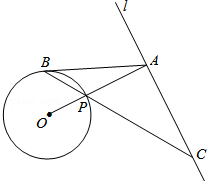 如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC.
如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com