
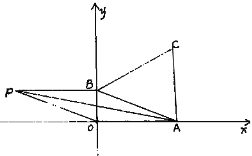
【题目】如图一次函数![]() 的图象与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等边三角形ABC,
的图象与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等边三角形ABC,
(1)求![]() ABC的面积。
ABC的面积。
(2)如果在第二象限内有一点P(![]() ),试用含有a的代数式表示四边形ABPO的面积,并求出当
),试用含有a的代数式表示四边形ABPO的面积,并求出当![]() ABP的面积与
ABP的面积与![]() ABC的面积相等时a的值。
ABC的面积相等时a的值。
(3)在x轴上,是否存在点M,使![]() MAB为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由。
MAB为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由。
【答案】(1)![]() ;(2)
;(2)![]() ,a=-
,a=-![]() ;(3)M1(2+
;(3)M1(2+![]() ,0)或M2(-
,0)或M2(-![]() ,0)或M3(
,0)或M3(![]() -2,0)或M4(
-2,0)或M4(![]() ,0).
,0).
【解析】
(1)由一次函数解析式可求出OA、OB的长度,在Rt△OAB中可求出AB的长度,再由等边三角形的性质可求出△ABC的面积;(2)依题意可得出S四边形ABPO=S△ABO+S△BOP,当S△ABP=S△ABC时求出a值.(3)①以AB为腰的等腰三角形有三个,②以AB为底边的等腰三角形有1一个,分别求出点M的坐标即可.
解:(1)∵函数解析式为:y=![]()
∴点B坐标为(0,1),点A坐标为(![]() ,0),
,0),
∴OA=![]() ,OB=1,
,OB=1,
在Rt△OAB中,AB=![]() =2,
=2,
则等边三角形ABC的面积为![]() AB2=
AB2=![]() .
.
(2)S四边形ABPO=S△ABO+S△BOP=![]() ×OA×OB+
×OA×OB+![]() ×OB×h=
×OB×h=![]() ×
×![]() ×1+
×1+![]() ×1×|a|.
×1×|a|.
∵P在第二象限,∴S四边形ABPO=![]() -
-![]() =
=![]() =
=![]() ,
,
S△ABP=SABPO-S△AOP=(![]() -
-![]() )-
)-![]() ×OA×
×OA×![]() .
.
∴S△ABP=![]() -
-![]() -
-![]() =
=![]() -
-![]() =S△ABC=
=S△ABC=![]() .
.
∴a=-![]() .
.
(3)(2)存在点M,使△MAB为等腰三角形
①若以AB为腰,如图所示:
当点M位于M1位置时,OM1=OA+AM1=OA+AB=2+![]() ,
,
此时点M1坐标为(2+![]() ,0);
,0);
当点M位于M2位置时,OM2=OA=![]() ,
,
此时点M2坐标为(-![]() ,0);
,0);
当点M位于M3位置时,OM3=AB=2,
此时点M3坐标为(![]() -2,0);
-2,0);
②若以AB为底边,如图所示:
作AB的中垂线交x轴于点M4,则此时△M4AB为等腰三角形,
∵OB=1,OA=![]() ,
,
∴∠OAB=30°,
∵AB=2,M4N是AB的中垂线,
∴AN=1,
在Rt△ANM4中,AM4=![]() =
=![]() ,
,
则OM4=OA-AM4=![]() ,
,
则此时M4的坐标为(![]() ,0).
,0).
综上可得存在点M,使△MAB为等腰三角形,点M的坐标为:M1(2+![]() ,0)或M2(-
,0)或M2(-![]() ,0)或M3(
,0)或M3(![]() -2,0)或M4(
-2,0)或M4(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.
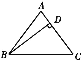
(1)证明:△BCD是直角三角形.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
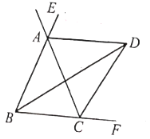
【题目】如图,![]() ,
,![]() ,
,![]() ,
,![]() 分别平分
分别平分![]() 的外角
的外角![]() ,内角
,内角![]() ,外角
,外角![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() ;⑤
;⑤![]() .其中正确的结论有______________.(把正确结论序号填写在横线上)
.其中正确的结论有______________.(把正确结论序号填写在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )

A.2:5 B.14:25 C.16:25 D.4:21
查看答案和解析>>
科目:初中数学 来源: 题型:
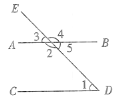
【题目】如图,直线AB,CD被DE所截,则∠1和 是同位角,∠1和 是内错角,∠1和 是同旁内角;
(2)在(1)中,如果∠5=∠1,那么∠1=∠3的推理过程如下,请在括号内注明理由:
因为∠5=∠1( ),
∠5=∠3( ),
所以∠1=∠3( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据 ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)填表:
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
|
(2)由上表你发现了什么规律?请用语言叙述这个规律:______________________________.
(3)根据你发现的规律填空:
①已知![]() =1.442,则
=1.442,则![]() =__________,
=__________,![]() =__________;
=__________;
②已知![]() =0.076 96,则
=0.076 96,则![]() =__________.
=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=50°,P 为 AB 中点,点 M 为射线 AC 上(不与点 A 重合)的任意一点,连接 MP, 并使MP 的延长线交射线BD 于点N,设∠BPN=α.

(1)求证:△APM≌△BPN;
(2)当 MN=2BN 时,求α的度数;
(3)若△BPN 为锐角三角形时,直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D为射线BA上一点,连接DC,且DC=BC.
(1)如图1,若DC⊥AC,AB= ![]() ,求CD的长;
,求CD的长;
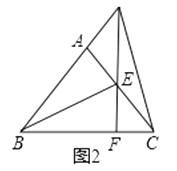
(2)如图2,若E为AC上一点,且CE=AD;连接BE,BE=2CE,连接DE并延长交BC于F.求证:DF=3EF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com