
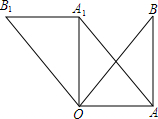
 如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°
如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°分析 (1)根据旋转的性质即可直接求解;
(2)根据旋转的性质以及平行线的判定定理证明B1A1∥OA且A1B1=OA即可证明四边形OAA1B1是平行四边形;
(3)利用平行四边形的面积公式求解.
解答 解:(1)A1B1=AB=6,∠AOA1=90°.
故答案是:6,90°;
(2)∵A1B1=AB=6,OA1-OA=6,∠OA1B1=∠OAB=90°,∠AOA1=90°,
∴∠OA1B1=∠AOA1,A1B1=OA,
∴B1A1∥OA,
∴四边形OAA1B1是平行四边形;
(3)S=OA•A1O=6×6=36.
即四边形OAA1B1的面积是36.
点评 本题考查了旋转的性质以及平行四边形的判定和面积公式,证明B1A1∥OA是关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:解答题
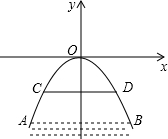 如图是以拱桥最高点为坐标原点,建立直角坐标系的抛物线拱桥.已知水在AB位置时,水面宽4$\sqrt{6}$米,水面距离桥顶12米.当水位上升达到警戒线CD时水面宽4$\sqrt{3}$米,若洪水到来时,水位以每小时0.6米速度上升.求水过警戒线后几小时淹到拱桥顶?
如图是以拱桥最高点为坐标原点,建立直角坐标系的抛物线拱桥.已知水在AB位置时,水面宽4$\sqrt{6}$米,水面距离桥顶12米.当水位上升达到警戒线CD时水面宽4$\sqrt{3}$米,若洪水到来时,水位以每小时0.6米速度上升.求水过警戒线后几小时淹到拱桥顶?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
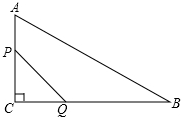 如图,△ABC中,∠C=90°,AC=12,BC=6,点P从A开始沿AC边向C点以1个单位每秒的速度移动.同时Q点从C沿边CB以2个单位每秒的速度向点B移动.设移动时间为t,请解答下列问题:
如图,△ABC中,∠C=90°,AC=12,BC=6,点P从A开始沿AC边向C点以1个单位每秒的速度移动.同时Q点从C沿边CB以2个单位每秒的速度向点B移动.设移动时间为t,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com