
【题目】如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以![]() cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC
cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC![]() CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )
CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )

A.  B.
B.  C.
C.  D.
D. 
【答案】D
【解析】
在△ABC中,∠C=90°,AC=BC=3cm,可得AB=![]() ,∠A=∠B=45°,分当0<x≤3(点Q在AC上运动,点P在AB上运动)和当3≤x≤6时(点P与点B重合,点Q在CB上运动)两种情况求出y与x的函数关系式,再结合图象即可解答.
,∠A=∠B=45°,分当0<x≤3(点Q在AC上运动,点P在AB上运动)和当3≤x≤6时(点P与点B重合,点Q在CB上运动)两种情况求出y与x的函数关系式,再结合图象即可解答.
在△ABC中,∠C=90°,AC=BC=3cm,可得AB=![]() ,∠A=∠B=45°,当0<x≤3时,点Q在AC上运动,点P在AB上运动(如图1), 由题意可得AP=
,∠A=∠B=45°,当0<x≤3时,点Q在AC上运动,点P在AB上运动(如图1), 由题意可得AP=![]() x,AQ=x,过点Q作QN⊥AB于点N,在等腰直角三角形AQN中,求得QN=
x,AQ=x,过点Q作QN⊥AB于点N,在等腰直角三角形AQN中,求得QN=![]() x,所以y=
x,所以y=![]() =
=![]() (0<x≤3),即当0<x≤3时,y随x的变化关系是二次函数关系,且当x=3时,y=4.5;当3≤x≤6时,点P与点B重合,点Q在CB上运动(如图2),由题意可得PQ=6-x,AP=3
(0<x≤3),即当0<x≤3时,y随x的变化关系是二次函数关系,且当x=3时,y=4.5;当3≤x≤6时,点P与点B重合,点Q在CB上运动(如图2),由题意可得PQ=6-x,AP=3![]() ,过点Q作QN⊥BC于点N,在等腰直角三角形PQN中,求得QN=
,过点Q作QN⊥BC于点N,在等腰直角三角形PQN中,求得QN=![]() (6-x),所以y=
(6-x),所以y=![]() =
=![]() (3≤x≤6),即当3≤x≤6时,y随x的变化关系是一次函数,且当x=6时,y=0.由此可得,只有选项D符合要求,故选D.
(3≤x≤6),即当3≤x≤6时,y随x的变化关系是一次函数,且当x=6时,y=0.由此可得,只有选项D符合要求,故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,AD为中线,点P是AD上一点,点Q是AC上一点,且∠BPQ+∠BAQ=180°.
(1)若∠ABP=α,求∠PQC的度数(用含α的式子表示);
(2)求证:BP=PQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,AP=DP,DE=DF,DE⊥AB于E,DF⊥AC于F,则下列结论:①.AD平分∠BAC;②.△BED≌△FPD;③.DP∥AB;④.DF是PC的垂直平分线.其中正确的是= _________ .(写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,先描出点![]() ,点
,点![]() .
.

(1)描出点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的位置,写出
的位置,写出![]() 的坐标 ;
的坐标 ;
(2)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);
(3)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() (保留作图痕迹).
(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题学习:设计概率模拟实验.
在学习概率时,老师说:“掷一枚质地均匀的硬币,大量重复实验后,正面朝上的概率约是![]() .”小海、小东、小英分别设计了下列三个模拟实验:
.”小海、小东、小英分别设计了下列三个模拟实验:
小海找来一个啤酒瓶盖(如图1)进行大量重复抛掷,然后计算瓶盖口朝上的次数与总次数的比值;
小东用硬纸片做了一个圆形转盘,转盘上分成8个大小一样的扇形区域,并依次标上1至8个数字(如图2),转动转盘10次,然后计算指针落在奇数区域的次数与总次数的比值;
小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子(如图3),其中有三枚是白子,一枚是黑子,从中随机同时摸出两枚棋子,并大量重复上述实验,然后计算摸出的两枚棋子颜色不同的次数与总次数的比值.

根据以上材料回答问题:
小海、小东、小英三人中,哪一位同学的实验设计比较合理,并简要说出其他两位同学实验的不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE.
求证:△ABC≌△ADE;(填空)
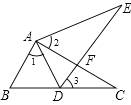
证明:∵∠2+∠E+∠AFE=180° ( )
∠3+∠C+∠CFD=180°(同理)
又∵∠2=∠3( )
∠AFE=∠CFD( )
∴∠E=_________.
∵∠1=∠2(已知)
∴∠1+∠CAD=∠2+∠_______.
即∠BAC=∠DAE
在△ABC和△ADE中
∴△ABC≌△ADE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F分别是正方形ABCD的边CD,AD上的点,CE=DF,AE,BF相交于点O.下列结论:①AE=BF;②AE⊥BF;③△ABF与△DAE成中心对称.其中,正确的结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠EDC=______°,∠AED=______°;
(2)线段DC的长度为何值时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,求∠BDA的度数;若不可以,请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com