
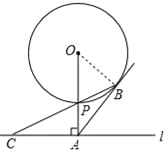
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)求证:AB=AC;
(2)若![]() ,求⊙O的半径.
,求⊙O的半径.

【答案】(1)证明见解析;(2)3.
【解析】
(1)由同圆半径相等和对顶角相等得∠OBP=∠APC,由圆的切线性质和垂直得∠ABP+∠OBP=90°和∠ACB+∠APC=90°,则∠ABP=∠ACB,根据等角对等边得AB=AC;
(2)设⊙O的半径为r,分别在Rt△AOB和Rt△ACP中根据勾股定理列等式,并根据AB=AC得52﹣r2=(2![]() )2﹣(5﹣r)2,求出r的值即可.
)2﹣(5﹣r)2,求出r的值即可.
解:(1)连接OB,∵OB=OP,∴∠OPB=∠OBP,∵∠OPB=∠APC,
∴∠OBP=∠APC,∵AB与⊙O相切于点B,∴OB⊥AB,∴∠ABO=90°,
∴∠ABP+∠OBP=90°,∵OA⊥AC,∴∠OAC=90°,∴∠ACB+∠APC=90°,∴∠ABP=∠ACB,
∴AB=AC;
(2)设⊙O的半径为r,在Rt△AOB中,AB2=OA2﹣OB2=52﹣r2,
在Rt△ACP中,AC2=PC2﹣PA2,AC2=(2![]() )2﹣(5﹣r)2,
)2﹣(5﹣r)2,
∵AB=AC,∴52﹣r2=(2![]() )2﹣(5﹣r)2,解得:r=3,
)2﹣(5﹣r)2,解得:r=3,
则⊙O的半径为3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在下列10×10的网格中,横、纵坐标均为整数的点叫做格点,例如A(3,0),B(4,3)都是格点.将△AOB绕点O顺时针旋转90°得到△COD(点A,B的对应点分别为点C,D).
(1)作出△COD;
(2)下面仅用无刻度的直尺画△AOD的内心I,操作如下:
第一步:在x轴上找一格点E,连接DE,使OE=OD;
第二步:在DE上找一点F,连接OF,使OF平分∠AOD;
第三步:找格点G,得到正方形OAGC,连接AC,则AC与OF的交点I是△OAD的内心.
请你按步骤完成作图,并直接写出E,F,I三点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
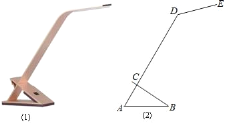
【题目】如图(1)是一种简易台灯,在其结构图(2)中灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.
(1)求DE与水平桌面(AB所在直线)所成的角;
(2)求台灯的高(点E到桌面的距离,结果精确到0.1cm).
(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,sin30°=0.5,cos30°=0.87,tan30°=0.58.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为进一步发展基础教育,自![]() 年以来加大了教育经费的投入,
年以来加大了教育经费的投入,![]() 年该地区投入教育经费
年该地区投入教育经费![]() 万元,
万元,![]() 年投入教育经费
年投入教育经费![]() 万元.
万元.
(1)求该地区这两年投入教育经费的年平均增长率;
(2)若该地区教育经费的投入还将保持相同的年平均增长率,请预算![]() 年该地区投入教育经费为 万元.
年该地区投入教育经费为 万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形ABC中,∠C=90°,点D是△ABC的重心,以AD为直角边作等腰Rt△ADE,若△ABC的周长为6,则△ADE的周长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线![]() 的顶点为点P,与y轴交于点B.点A坐标为(3,2).点M为抛物线上一动点,以点M为圆心,MA为半径的圆交x轴于C,D两点(点C在点D的左侧).
的顶点为点P,与y轴交于点B.点A坐标为(3,2).点M为抛物线上一动点,以点M为圆心,MA为半径的圆交x轴于C,D两点(点C在点D的左侧).

(1)如图②,当点M与点B重合时,求CD的长;
(2)当点M在抛物线上运动时,CD的长度是否发生变化?若变化,求出CD关于点M横坐标x的函数关系式;若不发生变化,求出CD的长;
(3)当△ACP与△ADP相似时,求出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2﹣3x+m=0的两实数根是( )
A. x1=1,x2=﹣1B. x1=1,x2=3C. x1=1,x2=2D. x1=1,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,是由北京国际数学家大会的会徽演化而成的图案,其主体部分是由一连串的等腰直角三角形依次连接而成,其中∠MA1A2=∠MA2A3…=∠MAnAn+1=90°,(n为正整数),若M点的坐标是(﹣1,2),A1的坐标是(0,2),则A22的坐标为( )

A.(﹣1﹣29,2﹣29)B.(1﹣29,2﹣29)
C.(﹣1﹣210,2﹣210)D.(1﹣210,2﹣210)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com