
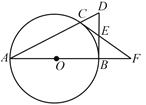
【题目】已知:如图,点C是以AB为直径的⊙O上一点,直线AC与过B点的切线相交于D,点E是BD的中点,直线CE交直线AB于点F.
(1)求证:CF是⊙O的切线;
(2)若ED=3,EF=5,求⊙O的半径.
【答案】(1)证明见解析;(2)6.
【解析】
(1)连CB、OC,根据切线的性质得∠ABD=90°,根据圆周角定理由AB是直径得到∠ACB=90°,即∠BCD=90°,则根据直角三角形斜边上的中线性质得CE=BE,于是得到∠OBC+∠CBE=∠OCB+∠BCE=90°,然后根据切线的判定定理得CF是⊙O的切线;
(2)CE=BE=DE=3,于是得到CF=CE+EF=4,然后根据相似三角形的性质即可得到结论.
(1)证明:连接![]() ,
,![]() ,
,
∵![]() 为⊙O的切线,
为⊙O的切线,![]() 是⊙O的直径,
是⊙O的直径,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() 为
为![]() 的中点,
的中点,
∴![]() .
.
∴![]() .
.
又∵![]()
∴![]() .
.
∴![]() .
.
∴![]() 是⊙O的切线.
是⊙O的切线.

(2)解:∵![]() ,
,![]()
∴![]()
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,即⊙O的半径为6
,即⊙O的半径为6


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
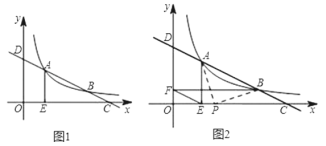
【题目】如图1,已知直线y=﹣![]() x+m与反比例函数y=
x+m与反比例函数y=![]() 的图象在第一象限内交于A、B两点(点A在点B的左侧),分别与x、y轴交于点C、D,AE⊥x轴于E.
的图象在第一象限内交于A、B两点(点A在点B的左侧),分别与x、y轴交于点C、D,AE⊥x轴于E.
(1)若OECE=12,求k的值.
(2)如图2,作BF⊥y轴于F,求证:EF∥CD.
(3)在(1)(2)的条件下,EF=![]() , AB=2
, AB=2![]() ,P是x轴正半轴上的一点,且△PAB是以P为直角顶点的等腰直角三角形,求P点的坐标.
,P是x轴正半轴上的一点,且△PAB是以P为直角顶点的等腰直角三角形,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
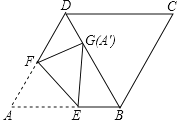
【题目】如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学完二次函数的图像及其性质后,老师让学生们说出![]() 的图像的一些性质,小亮说:“此函数图像开口向上,且对称轴是
的图像的一些性质,小亮说:“此函数图像开口向上,且对称轴是![]() ”;小丽说:“此函数肯定与x轴有两个交点”;小红说:“此函数与y轴的交点坐标为(0,-3)”;小强说:“此函数有最小值,
”;小丽说:“此函数肯定与x轴有两个交点”;小红说:“此函数与y轴的交点坐标为(0,-3)”;小强说:“此函数有最小值, ![]() ”……请问这四位同学谁说的结论是错误的( )
”……请问这四位同学谁说的结论是错误的( )
A. 小亮 B. 小丽 C. 小红 D. 小强
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年杭州市推出了“微公交”,“微公交”是国内首创的纯电动汽车租赁服务.它作为一种绿色出行方式,对缓解交通堵塞和停车困难,改善城市大气环境,都可以起到积极作用.据了解某租赁点拥有“微公交”![]() 辆.据统计,当每辆车的年租金为
辆.据统计,当每辆车的年租金为![]() 千元时可全部租出;每辆车的年租金每增加
千元时可全部租出;每辆车的年租金每增加![]() 千元,未租出的车将增加
千元,未租出的车将增加![]() 辆.
辆.
(1)当每辆车的年租金定为![]() 千元时,能租出多少辆?
千元时,能租出多少辆?
(2)当每辆车的年租金增加多少千元时,租赁公司的年收益(不计车辆维护等其他费用)可达到![]() 千元?
千元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点![]() 在第一象限,
在第一象限,![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,![]() ,
,![]() ,有一反比例函数图象刚好过点
,有一反比例函数图象刚好过点![]() .
.

(1)分别求出过点![]() 的反比例函数和过
的反比例函数和过![]() ,
,![]() 两点的一次函数的函数表达式;
两点的一次函数的函数表达式;
(2)直线![]() 轴,并从
轴,并从![]() 轴出发,以每秒
轴出发,以每秒![]() 个单位长度的速度向
个单位长度的速度向![]() 轴正方向运动,交反比例函数图象于点
轴正方向运动,交反比例函数图象于点![]() ,交
,交![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,当直线
,当直线![]() 运动到经过点
运动到经过点![]() 时,停止运动.设运动时间为
时,停止运动.设运动时间为![]() (秒).
(秒).
①问:是否存在![]() 的值,使四边形
的值,使四边形![]() 为平行四边形?若存在,求出
为平行四边形?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
②若直线![]() 从
从![]() 轴出发的同时,有一动点
轴出发的同时,有一动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向,以每秒
方向,以每秒![]() 个单位长度的速度运动.是否存在
个单位长度的速度运动.是否存在![]() 的值,使以点
的值,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形;若存在,求出
为顶点的四边形为平行四边形;若存在,求出![]() 的值,并进一步探究此时的四边形是否为特殊的平行四边形;若不存在,说明理由.
的值,并进一步探究此时的四边形是否为特殊的平行四边形;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(m+1)x+m2﹣3=0.
(1)当m取何值时,方程有两个不相等的实数根?
(2)设x1、x2是方程的两根,且(x1+x2)2﹣(x1+x2)﹣12=0,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为一座抛物线型的拱桥,AB、CD分别表示两个不同位置的水面宽度,O为拱桥顶部,水面AB宽为10米,AB距桥顶O的高度为12.5米,水面上升2.5米到达警戒水位CD位置时,水面宽为( )米.

A. 5 B. 2![]() C. 4
C. 4![]() D. 8
D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com