
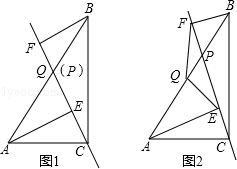
分析 (1)结合已知证明△BFQ≌△AEQ,进一步得到对角线互相平分即可;
(2)延长FQ交AE于点D,证明△FBQ≌△DAQ,结合直角三角形斜边中线等于斜边的一半即可.
解答 证明:(1)如图1,
∵点Q为AB中点,∴AQ=BQ.
∵BF⊥CP,AE⊥CP,
∴BF∥AE,∠BFQ=∠AEQ.
在△BFQ和△AEQ中,
$\left\{\begin{array}{l}{∠BFQ=∠AEQ}\\{∠BQF=∠AQE}\\{BQ=AQ}\end{array}\right.$,
∴△BFQ≌△AEQ(AAS).
∴QE=QF.
∴四边形AEBF是平行四边形;
(2)△QEF是等腰三角形,如图2,
延长FQ交AE于点D,
由(1)知AE∥BF,
∴∠QAD=∠FBQ.
在△FBQ和△DAQ中,
$\left\{\begin{array}{l}{∠FBQ=DAQ}\\{AQ=BQ}\\{∠BQF=∠AQD}\end{array}\right.$,
∴△FBQ≌△DAQ(ASA),
∴QF=QD.
∵AE⊥CP,
∴EQ是直角三角形DEF斜边上的中线,
∴QE=QF=QD,即QE=QF,
∴△QEF是等腰三角形.
点评 此题主要考查全等三角形的证明与应用,会组织全等三角形的条件,能分析题意构造全等三角形并证明运用是解题的关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
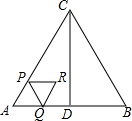 如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以2cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD-DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以2cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD-DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $±\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $±\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
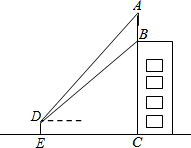 如图,某建筑物BC顶部接收塔AB,且点A,B,C在同一条直线上,小明在D处观接收塔顶部A的仰角为45°,观测旗杆底部B的仰角为30°.已知点D到地面的距离DE为1.7m,EC=30m,求接收塔AB的高度和建筑物BC的高度(结果保留根号).
如图,某建筑物BC顶部接收塔AB,且点A,B,C在同一条直线上,小明在D处观接收塔顶部A的仰角为45°,观测旗杆底部B的仰角为30°.已知点D到地面的距离DE为1.7m,EC=30m,求接收塔AB的高度和建筑物BC的高度(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com