
 如图,要使宽为2米的矩形平板车ABCD通过宽为2$\sqrt{2}$米的等宽的直角通道,平板车的长不能超过4米.
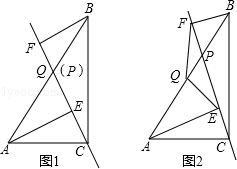
如图,要使宽为2米的矩形平板车ABCD通过宽为2$\sqrt{2}$米的等宽的直角通道,平板车的长不能超过4米. 分析 如图,先设平板手推车的长度不能超过x米,则得出x为最大值时,平板手推车所形成的三角形CBP为等腰直角三角形.连接PO,与BC交于点N,利用△CBP为等腰直角三角形即可求得平板手推车的长度不能超过多少米.
解答 解:设平板手推车的长度不能超过x米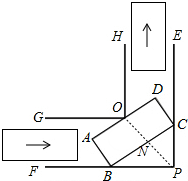
则x为最大值,且此时平板手推车所形成的三角形CBP为等腰直角三角形.
连接PO,与BC交于点N.
∵直角走廊的宽为2$\sqrt{2}$m,
∴PO=4m,
∴NP=PO-ON=4-2=2(m).
又∵△CBP为等腰直角三角形,
∴AD=BC=2CN=2NP=4(m).
故答案为:4
点评 本题主要考查了勾股定理的应用以及等腰三角形知识,解答的关键是由题意得出要想顺利通过直角走廊,此时平板手推车所形成的三角形为等腰直角三角形.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,二次函数y=$\frac{1}{3}{x^2}$+bx+c的图象与y轴交于点A,与双曲线y=$\frac{8}{x}$有一个公共点B,它的横坐标为4,过点B作直线l∥x轴,与该二次函数图象交于另一个点C,直线AC在y轴上的截距是-6.
如图,在平面直角坐标系xOy中,二次函数y=$\frac{1}{3}{x^2}$+bx+c的图象与y轴交于点A,与双曲线y=$\frac{8}{x}$有一个公共点B,它的横坐标为4,过点B作直线l∥x轴,与该二次函数图象交于另一个点C,直线AC在y轴上的截距是-6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,边长等于4的正方形ABCD两个顶点A与D分别在x轴和y轴上滑动(A、D都不与坐标原点O重合),作CE⊥x轴,垂足为E,当OA等于2$\sqrt{2}$时,四边形OACE面积最大.
如图,边长等于4的正方形ABCD两个顶点A与D分别在x轴和y轴上滑动(A、D都不与坐标原点O重合),作CE⊥x轴,垂足为E,当OA等于2$\sqrt{2}$时,四边形OACE面积最大.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
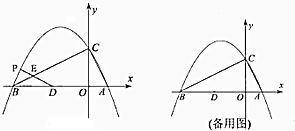
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com