
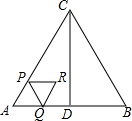
 如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以2cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD-DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以2cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD-DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).分析 (1)易证△APQ是等边三角形,即可得到QR=PQ=AP=2t;
(2)过点A作AG⊥BC于点G,如图②,易得点R运动的路程长是AG+CG,只需求出AG、CG就可解决问题;
(3)四边形APRQ与△ACD重叠部分图形可能是菱形,也可能是五边形,故需分情况讨论,然后运用割补法就可解决问题;
(4)由于直角顶点不确定,故需分情况讨论,只需分∠QRB=90°和∠RQB=90°两种情况讨论,即可解决问题.
解答 解:(1)如图①,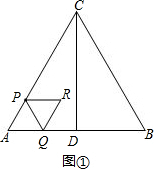
∵△ABC是等边三角形,
∴∠ACB=∠B=60°.
∵PQ∥BC,
∴∠APQ=∠ACB=60°,∠AQP=∠B=60°,
∴△APQ是等边三角形.
∴PQ=AP=2t.
∵△PQR是等边三角形,
∴QR=PQ=2t;
(2)过点A作AG⊥BC于点G,如图②,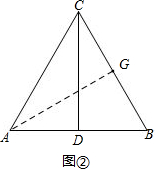
则点R运动的路程长是AG+CG.
在Rt△AGC中,∠AGC=90°,sin60°=$\frac{AG}{AC}$=$\frac{\sqrt{3}}{2}$,cos60°=$\frac{CG}{AC}$=$\frac{1}{2}$,AC=4,
∴AG=2$\sqrt{3}$,CG=2.
∴点R运动的路程长2$\sqrt{3}$+2;
(3)①当0<t≤$\frac{2}{3}$时,如图③,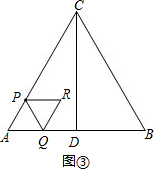
S=S菱形APRQ=2×S正△APQ=2×$\frac{\sqrt{3}}{4}$×(2t)2=2$\sqrt{3}$t2;
②当$\frac{2}{3}$<t≤1时,如图④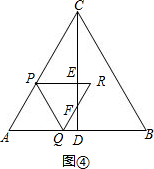
PE=PC•sin∠PCE=(4-2t)×$\frac{1}{2}$=2-t,
∴ER=PR-PE=2t-(2-t)=3t-2,
∴EF=ER•tanR=$\sqrt{3}$(3t-2)
∴S=S菱形APRQ-S△REF
=2$\sqrt{3}$t2-$\frac{\sqrt{3}}{2}$(3t-2)2=-$\frac{5\sqrt{3}}{2}$t2+6$\sqrt{3}$t-2$\sqrt{3}$;
(3)t=$\frac{2}{3}$或t=$\frac{4}{3}$
提示:①当∠QRB=90°时,如图⑤,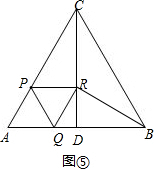
cos∠RQB=$\frac{QR}{QB}$=$\frac{1}{2}$,
∴QB=2QR=2QA,
∴AB=3QA=6t=4,
∴t=$\frac{2}{3}$;
②当∠RQB=90°时,如图⑥,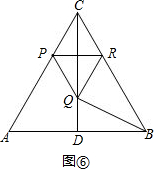
同理可得BC=3RC=3PC=3(4-2t)=4,
∴t=$\frac{4}{3}$.
点评 本题主要考查了等边三角形的判定与性质、特殊角的三角函数值、等边三角形的面积公式(等边三角形的面积等于边长平方的$\frac{\sqrt{3}}{4}$倍)等知识,运用分类讨论的数学思想是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
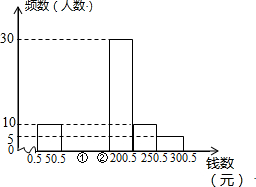 某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.
某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.| 分 组 | 频数 | 所占比例 |
| 0.5~50.5 | 10 | 0.1 |
| 50.5~100.5 | 20 | 0.2 |
| 100.5~150.5 | 35 | 35 |
| 150.5~200.5 | 30 | 0.3 |
| 200.5~250.5 | 10 | 0.1 |
| 250.5~300.5 | 5 | 0.05 |
| 合 计 | 100 | ------ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
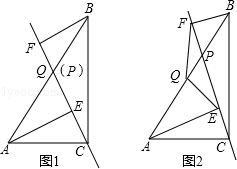
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,边长等于4的正方形ABCD两个顶点A与D分别在x轴和y轴上滑动(A、D都不与坐标原点O重合),作CE⊥x轴,垂足为E,当OA等于2$\sqrt{2}$时,四边形OACE面积最大.
如图,边长等于4的正方形ABCD两个顶点A与D分别在x轴和y轴上滑动(A、D都不与坐标原点O重合),作CE⊥x轴,垂足为E,当OA等于2$\sqrt{2}$时,四边形OACE面积最大.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
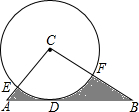 如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )| A. | $\frac{32}{3}\sqrt{3}-4π$ | B. | $\frac{32}{3}\sqrt{3}-2π$ | C. | 16-4π | D. | 16-2π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
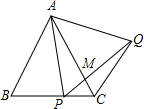 如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )| A. | 只有①② | B. | 只有①③ | C. | 只有①②③ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com