
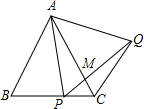
 如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )| A. | 只有①② | B. | 只有①③ | C. | 只有①②③ | D. | ①②③④ |
分析 根据等边三角形性质得出AB=AC,AP=AQ,∠BAC=∠B=∠PAQ=60°,求出∠BAP=∠CAQ,根据SAS证△ABP≌△ACQ,推出∠ACQ=∠B=60°=∠BAC,根据平行线的判定推出即可,再根据等腰三角形性质求出∠BAP=30°,求出∠PMA=90°,即可得出答案.
解答 证明:如图,∵△ABC和△APQ是等边三角形,
∴AB=AC,AP=AQ,∠BAC=∠B=∠PAQ=60°,
∴∠BAP=∠CAQ=60°-∠PAC,
在△ABP和△ACQ中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAP=∠CAQ}\\{AP=AQ}\end{array}\right.$,
∴△ABP≌△ACQ(SAS),
∴∠ACQ=∠B=60°=∠BAC,故②正确,
∴AB∥CQ,故①正确,
∵∠APQ=∠ACQ=60°,∠PAC=∠PAC,
∴△APM∽△ACP,
∴$\frac{AP}{AC}=\frac{AM}{AP}$,
∴AP2=AC•AM,故③正确,
∵BP=PC,
∴∠BAP=30°,
∴∠PAC=30°,
∵∠APM=60°,
∴∠AMP=90°,
∴PQ⊥AC,故④正确.
故选D.
点评 本题考查了相似三角形的判定和性质,等边三角形性质,全等三角形的性质和判定,平行线性质和判定,等腰三角形性质的应用,主要考查学生的推理能力.


科目:初中数学 来源: 题型:解答题
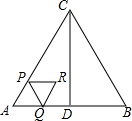 如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以2cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD-DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以2cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD-DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| Ⅰ | Ⅱ | |
| 成本(元/瓶) | 60 | 70 |
| 利润(元/瓶) | 30 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
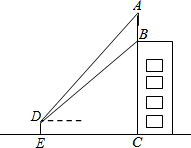 如图,某建筑物BC顶部接收塔AB,且点A,B,C在同一条直线上,小明在D处观接收塔顶部A的仰角为45°,观测旗杆底部B的仰角为30°.已知点D到地面的距离DE为1.7m,EC=30m,求接收塔AB的高度和建筑物BC的高度(结果保留根号).
如图,某建筑物BC顶部接收塔AB,且点A,B,C在同一条直线上,小明在D处观接收塔顶部A的仰角为45°,观测旗杆底部B的仰角为30°.已知点D到地面的距离DE为1.7m,EC=30m,求接收塔AB的高度和建筑物BC的高度(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
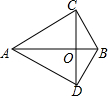 如图,△ABC中,∠ACB=90°,∠BAC=30°,将线段AC绕点A顺时针旋转60°得到线段AD,连接CD交AB于点O,连接BD.
如图,△ABC中,∠ACB=90°,∠BAC=30°,将线段AC绕点A顺时针旋转60°得到线段AD,连接CD交AB于点O,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
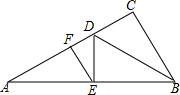 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,DE⊥AB于E,EF∥BC交AC于F.
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,DE⊥AB于E,EF∥BC交AC于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com