
分析 (1)根据“当每个台灯售价为40元时,平均每月售出600个;若售价每上涨1元,其月销售量就减少20个”列出代数式;
(2)方法一:设每个台灯的售价为x元.根据每个台灯的利润×销售数量=总利润列出方程并解答;
方法二:设每个台灯降价x元.根据每个台灯的利润×销售数量=总利润列出方程并解答;
(3)解题思路同(2).
解答 解:(1)依题意得:600-20x.
故答案是:600-20x.
(2)方法一:
设每个台灯的售价为x元.
根据题意,得(x-30)[(40-x)×200+600]=8400,
解得x1=36(舍),x2=37.
当x=36时,(40-36)×200+600=1400>1210;
当x=37时,(40-37)×200+600=1200<1210;
答:每个台灯的售价为37元.
方法二:
设每个台灯降价x元.
根据题意,得(40-x-30)(200x+600)=8400,
解得x1=3,x2=4(舍).
当x=3时,40-3=37,(40-37)×200+600=1200<1210;
当x=4时,40-3=36,(40-36)×200+600=1400>1210;
答:每个台灯的售价为37元;
(3)设每个台灯的售价为x元.
根据题意,得(x-30)[(40-x)×200+600]=8000,
解得x1=38,x2=50.
答:每个台灯的售价为38元或50元.
点评 本题考查了一元二次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,点D,E分别在AB,AC上,∠AED=∠ABC.
如图,在△ABC中,点D,E分别在AB,AC上,∠AED=∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=x2+mx+n-1的对称轴为x=2.
在平面直角坐标系xOy中,抛物线y=x2+mx+n-1的对称轴为x=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
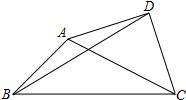 已知△ABC中,∠ABC=45°,AB=7$\sqrt{2}$,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为$\frac{25\sqrt{2}}{2}$.
已知△ABC中,∠ABC=45°,AB=7$\sqrt{2}$,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为$\frac{25\sqrt{2}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com