
 如图,反比例函数y=$\frac{k}{x}$的图象经过点(-1,-2$\sqrt{2}$),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.
如图,反比例函数y=$\frac{k}{x}$的图象经过点(-1,-2$\sqrt{2}$),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.分析 (1)把点(-1,-2$\sqrt{2}$)代入反比例函数y=$\frac{k}{x}$,求出k即可;
(2)连接OC,作AM⊥x轴于M,CN⊥x轴于N,则AM∥CN,∠AMO=∠ONC=90°,先由AAS证明△OAM≌△CON,得出OM=CN,AM=ON,再由三角形的角平分线性质得出$\frac{AP}{CP}=\frac{AB}{BC}$=$\frac{\sqrt{2}}{1}$,根据平行线的性质得出比例式:$\frac{AM}{CN}=\frac{AP}{CP}$=$\frac{\sqrt{2}}{1}$,设CN=OM=x,则AM=ON=$\sqrt{2}$x,根据题意得出方程:x•$\sqrt{2}$x=2$\sqrt{2}$,解方程求出CN、ON,即可得出点C的坐标.
解答 解:(1)把点(-1,-2$\sqrt{2}$)代入反比例函数y=$\frac{k}{x}$得:
k=-1×(-2$\sqrt{2}$)=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$;
(2)连接OC,作AM⊥x轴于M,CN⊥x轴于N,如图所示: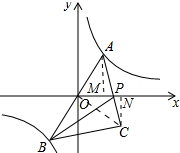 则AM∥CN,∠AMO=∠ONC=90°,
则AM∥CN,∠AMO=∠ONC=90°,
∴∠AOM+∠OAM=90°,
根据题意得:点A和点B关于原点对称,
∴OA=OB,
∵△ABC是等腰直角三角形,AB为斜边,
∴OC⊥AB(三线合一),OC=$\frac{1}{2}$AB=OA,AC=BC,AB=$\sqrt{2}$BC,
∴∠AOC=90°,
即∠AOM+∠CON=90°,
∴∠OAM=∠CON,
在△OAM和△CON中,
$\left\{\begin{array}{l}{∠AMO=∠ONC}&{\;}\\{∠OAM=∠CON}&{\;}\\{OA=OC}&{\;}\end{array}\right.$,
∴△OAM≌△CON(AAS),
∴OM=CN,AM=ON,
∵BP平分∠ABC,
∴$\frac{AP}{CP}=\frac{AB}{BC}$=$\frac{\sqrt{2}}{1}$,
∵AM∥CN,
∴$\frac{AM}{CN}=\frac{AP}{CP}$=$\frac{\sqrt{2}}{1}$,
设CN=OM=x,则AM=ON=$\sqrt{2}$x,
∵点A在反比例函数y=$\frac{2\sqrt{2}}{x}$上,
∴OM•AM=2$\sqrt{2}$,
即x•$\sqrt{2}$x=2$\sqrt{2}$,
解得:x=$\sqrt{2}$,
∴CN=$\sqrt{2}$,ON=2,
∴点C的坐标为:(2,-$\sqrt{2}$);
故答案为::(2,-$\sqrt{2}$).
点评 本题是反比例函数综合题目,考查了用待定系数法求反比例函数解析式、等腰直角三角形的性质、全等三角形的判定与性质、三角形的角平分线性质、平行线的性质等知识;本题难度较大,综合性强,特别是(2)中,需要通过作辅助线证明三角形全等和运用三角形的角平分线的性质才能得出结果.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题
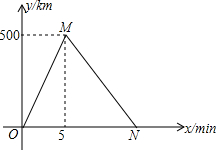 小亮和小华的家住在滨河大道旁,周六早上,他们两个相约去滨河大道上训练跑步,他们从A路口出发,沿滨河大道跑到B路口再原路返回,因为体力的原因,他们返回的平均速度都是各自出发时速度的$\frac{4}{5}$,设出发时间为x min,距A路口的距离为y cm,图中折线表示小亮在整个训练过程中y与x之间的函数关系图象.
小亮和小华的家住在滨河大道旁,周六早上,他们两个相约去滨河大道上训练跑步,他们从A路口出发,沿滨河大道跑到B路口再原路返回,因为体力的原因,他们返回的平均速度都是各自出发时速度的$\frac{4}{5}$,设出发时间为x min,距A路口的距离为y cm,图中折线表示小亮在整个训练过程中y与x之间的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
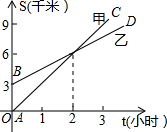 如图,已知A地在B地的正南方3千米处,甲、乙两人同时分别从A、B两地向正北方向匀速行驶,他们与A地的而距离(千米)与所行的时间(时)之间的函数关系如图中AC和BD所示,当他们行驶了4小时后,他们之间的距离为3千米.
如图,已知A地在B地的正南方3千米处,甲、乙两人同时分别从A、B两地向正北方向匀速行驶,他们与A地的而距离(千米)与所行的时间(时)之间的函数关系如图中AC和BD所示,当他们行驶了4小时后,他们之间的距离为3千米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -11 | -2 | 1 | -2 | -5 | … |
| A. | -11 | B. | -2 | C. | 1 | D. | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
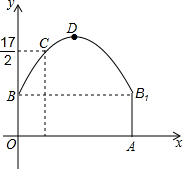 如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=-$\frac{1}{6}$x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为$\frac{17}{2}$m.
如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=-$\frac{1}{6}$x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为$\frac{17}{2}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
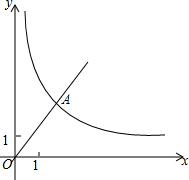 已知:如图,在平面直角坐标系xOy中,正比例函数y=$\frac{4}{3}$x的图象经过点A,点A的纵坐标为4,反比例函数y=$\frac{m}{x}$的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB.求:
已知:如图,在平面直角坐标系xOy中,正比例函数y=$\frac{4}{3}$x的图象经过点A,点A的纵坐标为4,反比例函数y=$\frac{m}{x}$的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com