
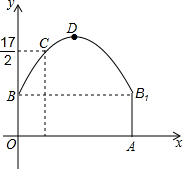
 ��ͼ�������Ľ����������ߺͳ����ι��ɣ������εij���12m������4m������ͼ����ʾ��ֱ������ϵ�������߿�����y=-$\frac{1}{6}$x2+bx+c��ʾ���������ߵĵ�C��ǽ��OB��ˮƽ����Ϊ3mʱ��������OA�ľ���Ϊ$\frac{17}{2}$m��
��ͼ�������Ľ����������ߺͳ����ι��ɣ������εij���12m������4m������ͼ����ʾ��ֱ������ϵ�������߿�����y=-$\frac{1}{6}$x2+bx+c��ʾ���������ߵĵ�C��ǽ��OB��ˮƽ����Ϊ3mʱ��������OA�ľ���Ϊ$\frac{17}{2}$m������ ��1����ȷ��B���C�����꣬Ȼ�����ô���ϵ������������߽���ʽ���������䷽��ȷ������D�����꣬�Ӷ��õ���D������OA�ľ��룻
��2�����������ߵĶԳ���Ϊֱ��x=6������������˫���г���������Ϊ4m���������������������OA�Ľ���Ϊ��2��0����10��0����Ȼ������Ա���Ϊ2��10�ĺ���ֵ���ٰѺ���ֵ��6���д�С�Ƚϼ����жϣ�
��3�������߿������£�����ֵԽ�ԳƵ�֮��ľ���ԽС�����Ǽ��㺯��ֵΪ8����Ӧ���Ա�����ֵ���ɵõ����ŵƵ�ˮƽ������Сֵ��
��� �⣺��1�����������B��0��4����C��3��$\frac{17}{2}$����
��B��0��4����C��3��$\frac{17}{2}$������y=-$\frac{1}{6}$x2+bx+c��$\left\{\begin{array}{l}{c=4}\\{-\frac{1}{6}��{3}^{2}+3b+c=\frac{17}{2}}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=2}\\{c=4}\end{array}\right.$��
���������߽���ʽΪy=-$\frac{1}{6}$x2+2x+4��
��y=-$\frac{1}{6}$��x-6��2+10��
����D��6��10����
���Թ���D������OA�ľ���Ϊ10m��
��2��������û�����������������OA�Ľ���Ϊ��2��0����10��0����
��x=2��x=10ʱ��y=$\frac{22}{3}$��6��
�������������ܰ�ȫͨ����
��3����y=8����-$\frac{1}{6}$��x-6��2+10=8�����x1=6+2$\sqrt{3}$��x2=6-2$\sqrt{3}$��
��x1-x2=4$\sqrt{3}$��
�������ŵƵ�ˮƽ������С��4$\sqrt{3}$m��
���� ���⿼���˶��κ�����Ӧ�ã��������κ���ģ�ͽ��ʵ�����⣬���ö��κ�������������ε����������ź��ŵ�ʵ������ʱ��Ҫǡ���ذ���Щʵ�������е�������ʵ��ƽ��ֱ������ϵ�е��������ϣ��Ӷ�ȷ�������ߵĽ���ʽ��ͨ������ʽ�ɽ��һЩ����������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������ | B�� | ���� | C�� | ���� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������������y=$\frac{k}{x}$��ͼ���㣨-1��-2$\sqrt{2}$������A�Ǹ�ͼ���һ����֧�ϵĶ��㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪб��������ֱ��������ABC������C�ڵ������ޣ�AC��x�ύ�ڵ�P������BP��
��ͼ������������y=$\frac{k}{x}$��ͼ���㣨-1��-2$\sqrt{2}$������A�Ǹ�ͼ���һ����֧�ϵĶ��㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪб��������ֱ��������ABC������C�ڵ������ޣ�AC��x�ύ�ڵ�P������BP���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x1��x2��x3 | B�� | x1��x3��x2 | C�� | x2��x1��x3 | D�� | x2��x3��x1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a=3��b=1 | B�� | a=-3��b=1 | C�� | a=3��b=-1 | D�� | a=-3��b=-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��x2-8�� | B�� | 2��x-2��2 | C�� | 2��x+2����x-2�� | D�� | 2x��x-$\frac{4}{x}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ʵ��a��b�������϶�Ӧ�ĵ��λ����ͼ��ʾ������|a-b|�Ľ��Ϊ��������
ʵ��a��b�������϶�Ӧ�ĵ��λ����ͼ��ʾ������|a-b|�Ľ��Ϊ��������| A�� | a+b | B�� | a-b | C�� | b-a | D�� | -a-b |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com