
分析 (1)先计算判别式的值得到△=4k2-12k+9,配方得到△=(2k-3)2,根据非负数的性质易得△≥0,则根据判别式的意义即可得到结论;
(2)分类讨论:当b=c时,则△=(2k-3)2=0,解得k=$\frac{3}{2}$,然后解方程得到b=c=2,根据三角形三边关系可判断这种情况不符号条件;当a=b=4或a=c=4时,把x=4代入方程可解得k=$\frac{5}{2}$,则方程化为x2-6x+8=0,解得x1=4,x2=2,所以a=b=4,c=2或a=c=4,b=2,然后计算△ABC的周长.
解答 (1)证明:△=(2k+1)2-4×4(k-$\frac{1}{2}$)
=4k2+4k+1-16k+8,
=4k2-12k+9
=(2k-3)2,
∵(2k-3)2≥0,即△≥0,
∴无论k取何值,这个方程总有实数根;
(2)解:当b=c时,△=(2k-3)2=0,解得k=$\frac{3}{2}$,方程化为x2-4x+4=0,解得b=c=2,而2+2=4,故舍去;
当a=b=4或a=c=4时,把x=4代入方程得16-4(2k+1)+4(k-$\frac{1}{2}$)=0,解得k=$\frac{5}{2}$,方程化为x2-6x+8=0,解得x1=4,x2=2,即a=b=4,c=2或a=c=4,b=2,
所以△ABC的周长=4+4+2=10.
点评 本题考查了根的判别式:用一元二次方程根的判别式(△=b2-4ac)判断方程的根的情况:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了等腰三角形的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件赢利40元,为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加赢利,尽快减少库存.经市场调查发现:如果每件童装降价4元,那么平均每天就可多售出8件.要想平均每天销售这种童装赢利1200元,那么每件童装应降价多少元?
百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件赢利40元,为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加赢利,尽快减少库存.经市场调查发现:如果每件童装降价4元,那么平均每天就可多售出8件.要想平均每天销售这种童装赢利1200元,那么每件童装应降价多少元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
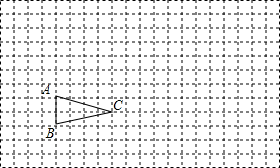 作图题:如图所示,△ABC在方格纸中
作图题:如图所示,△ABC在方格纸中查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com