
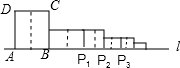
 如图,正方形ABCD的边长为1,AB边与直线l重合,沿AB边的中垂线将正方形剪开,剪开后的右侧部分以B为中心,顺时针旋转90°得到BP1为边的新矩形,我们称之为第1次操作,沿BP1边的中垂线将矩形剪开,再将剪开后的右侧部分以P1为中心顺时针旋转90°,得到P1P2为边的正方形,我们称之为第2次操作…按此规律继续操作下去,AP2015的长是$\frac{{2}^{1008}-1}{{2}^{1006}}$.
如图,正方形ABCD的边长为1,AB边与直线l重合,沿AB边的中垂线将正方形剪开,剪开后的右侧部分以B为中心,顺时针旋转90°得到BP1为边的新矩形,我们称之为第1次操作,沿BP1边的中垂线将矩形剪开,再将剪开后的右侧部分以P1为中心顺时针旋转90°,得到P1P2为边的正方形,我们称之为第2次操作…按此规律继续操作下去,AP2015的长是$\frac{{2}^{1008}-1}{{2}^{1006}}$. 分析 根据旋转的性质和矩形的性质易得AB=1,BP1=1,P1P2=$\frac{1}{2}$,P2P3=$\frac{1}{2}$,P3P4=($\frac{1}{2}$)2,P4P5=($\frac{1}{2}$)2,P5P6=($\frac{1}{2}$)3,P6P7=($\frac{1}{2}$)3,根据P的脚标数与$\frac{1}{2}$的指数的关系易得P2013P2014=($\frac{1}{2}$)1007,P2014P2015=($\frac{1}{2}$)1007,所以AP2015=3+$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)1006,接着利用方程的思想计算出$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)1006=1-($\frac{1}{2}$)1006,则AP2015=4-($\frac{1}{2}$)1006.
解答 解:AB=1,BP1=1,
P1P2=$\frac{1}{2}$,P2P3=$\frac{1}{2}$,
P3P4=($\frac{1}{2}$)2,P4P5=($\frac{1}{2}$)2,
P5P6=($\frac{1}{2}$)3,P6P7=($\frac{1}{2}$)3,
…
P2013P2014=($\frac{1}{2}$)1007,P2014P2015=($\frac{1}{2}$)1007,
所以AP2015=2×1+2[$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)1007]=3+$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)1006,
设$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)1006=S,
则1+$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)1005=2S,
所以S=1-($\frac{1}{2}$)1006,
所以AP2015=3+1-($\frac{1}{2}$)1006=$\frac{{2}^{1008}-1}{{2}^{1006}}$.
故答案为=$\frac{{2}^{1008}-1}{{2}^{1006}}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查通过从特殊到一般解决规律型问题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:解答题
| 6,8,10 | 8,15,17 | 10,24,26 | … | 20,b,c |
| 62+82=102 | 82+152=172 | 102+242=262 | … | 202+b2=c2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
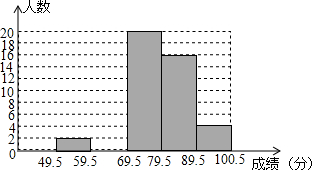 我校艺术节期间,开展了“巴蜀好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布表和频数分布直方图(如图),请你根据图表提供的信息,解答下列问题:
我校艺术节期间,开展了“巴蜀好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布表和频数分布直方图(如图),请你根据图表提供的信息,解答下列问题:| 分组 | 74.5~79.5 | 79.5~84.5 | 84.5~89.5 | 89.5~94.5 | 94.5~100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
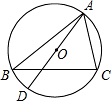 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为$\frac{3}{2}$,AC=2,则sinB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为$\frac{3}{2}$,AC=2,则sinB的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com