
����Ŀ����ͼ������ABC�У�AB=5��AC=9��S��ABC=![]() ������P��A�������������AB������ÿ��5����λ���ٶ��˶�������Q��C�����������ͬ���ٶ����߶�AC����C��A�˶�����Q���˶���A��ʱ��P��Q����ͬʱֹͣ�˶�����PQΪ����������PQEF��P��Q��E��F����ʱ��������CQΪ����AC�Ϸ���������QCGH��
������P��A�������������AB������ÿ��5����λ���ٶ��˶�������Q��C�����������ͬ���ٶ����߶�AC����C��A�˶�����Q���˶���A��ʱ��P��Q����ͬʱֹͣ�˶�����PQΪ����������PQEF��P��Q��E��F����ʱ��������CQΪ����AC�Ϸ���������QCGH��
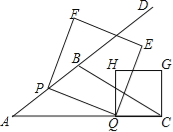
��1����tanA��ֵ��
��2�����P�˶�ʱ��Ϊt��������PQEF�����ΪS����̽��S�Ƿ������Сֵ�������ڣ���������Сֵ���������ڣ���˵�����ɣ�
��3����tΪ��ֵʱ��������PQEF��ij�����㣨Q����⣩����������QCGH�ı��ϣ���ֱ��д��t��ֵ��
���𰸡���1��![]() ����2�����ڣ�S��Сֵ=
����2�����ڣ�S��Сֵ=![]() ����3��t1=
����3��t1=![]() ��t2=
��t2=![]() ��t3=1��t4=
��t3=1��t4=![]() ��
��
��������
���⣨1����ͼ1������B��BM��AC�ڵ�M��������������BM�ij��ȣ����ù��ɶ����õ�AM�ij��ȣ������������Ǻ����Ķ�����н��
��2����ͼ2������P��PN��AC�ڵ�N�����ã�1���еĽ��ۺ��ɶ����õ�PN2+NQ2=PQ2�������������ε������ʽ�õ�S����t�Ķ��κ��������ö��κ����Ķ������깫ʽ�Ͷ��κ���ͼ���������������ֵ��
��3����Ҫ�������ۣ�����E�ڱ�HG�ϡ���F�ڱ�HG�ϡ���P��QH�����E��QC�ϣ�����F��C��ʱ���Ӧ��t��ֵ��
����������⣺��1����ͼ1������B��BM��AC�ڵ�M��
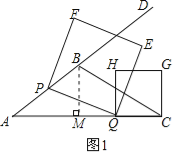
��AC=9��S��ABC=![]() ��
��
��![]() ACBM=
ACBM=![]() ����
����![]() ��9BM=
��9BM=![]() ��
��
���BM=3��
�ɹ��ɶ�������
AM=![]() =
=![]() =4��
=4��
��tanA=![]() =
=![]() ��
��
��2�����ڣ�
��ͼ2������P��PN��AC�ڵ�N��

�������AP=CQ=5t��
��tanA=![]() ��
��
��AN=4t��PN=3t��
��QN=AC��AN��CQ=9��9t��
���ݹ��ɶ����õ���PN2+NQ2=PQ2��
S������PQEF=PQ2=��3t��2+��9��9t��2=90t2��162t+81��0��t��![]() ����
����
�ߩ�/span>![]() =
=![]() =
=![]() ��t��ȡֵ��Χ֮�ڣ�
��t��ȡֵ��Χ֮�ڣ�
��S��Сֵ=![]() =
=![]() =
=![]() ��
��
��3��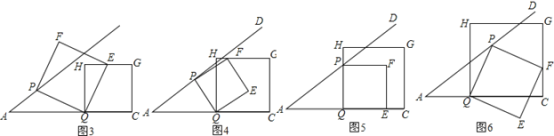
����ͼ3������E�ڱ�HG��ʱ��t1=![]() ��
��
����ͼ4������F�ڱ�HG��ʱ��t2=![]() ��
��
����ͼ5������P��QH�����E��QC�ϣ�ʱ��t3=1
����ͼ6������F��C��ʱ��t4=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() �������ύ��A��B���㣬������AO����һ��P������APB����APΪ���ĵ���������ʱ����P��������________________.
�������ύ��A��B���㣬������AO����һ��P������APB����APΪ���ĵ���������ʱ����P��������________________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
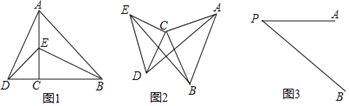
����Ŀ��(1)���ⷢ��
��ͼ1,��ACB����DCE��Ϊ����ֱ��������,��ACB=90��,B,C,D��һ��ֱ����.
���:�߶�AD,BE֮��Ĺ�ϵΪ .
(2)��չ̽��
��ͼ2,��ACB����DCE��Ϊ����ֱ��������,��ACB=��DCE=90��,���ж�AD,BE�Ĺ�ϵ,��˵������.
(3)�������
��ͼ3,�߶�PA=3,��B���߶�PA��һ��,PB=5,����AB,��AB�Ƶ�A��ʱ����ת90��õ��߶�AC,���ŵ�B��λ�õı仯,ֱ��д��PC�ķ�Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
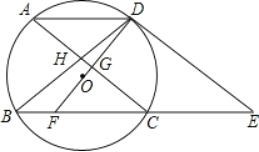
����Ŀ����ͼ����O����AD��BC������D�����߽�BC���ӳ����ڵ�E��AC��DE��BD�ڵ�H��DO���ӳ��߷ֱ�AC��BC�ڵ�G��F��
(1)��֤��DF��ֱƽ��AC��
(2)��֤��FC��CE��
(3)����AD��5cm��AC��8cm������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�����A�ͺ�B�����ֵ��ԣ�����A�͵���ÿ̨������Ϊ400Ԫ��B�͵���ÿ̨������Ϊ500Ԫ�����̵�ƻ���һ���Թ��������ͺŵĵ��Թ�100̨������B�͵��ԵĽ�����������A�͵��Ե�2�����蹺��A�͵���x̨����100̨���Ե�����������ΪyԪ��
��1����y����x�ĺ�����ϵʽ��
��2�����̵깺��A�͡�B�͵��Ը�����̨������ʹ���������������������Ƕ��٣�
��3��ʵ�ʽ���ʱ�����Ҷ�A�͵��Գ������µ�a��0��a��200��Ԫ�������̵�����A�͵���60̨�����̵걣��ͬ�ֵ��Ե��ۼ۲��䣬�������������Ϣ����Ƴ�ʹ��100̨�����������������Ľ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
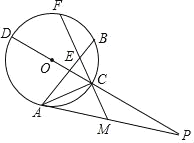
����Ŀ����ͼ��CD�ǡ�O��ֱ������AΪԲ��һ�㲻��C��D���غϣ�����A����O�����ߣ���DC���ӳ��߽��ڵ�P����MΪAP��һ�㣬����MC���ӳ������O���ڵ�F��EΪCF��һ�㣬��MA��ME������AE���ӳ������O�ڵ�B������BC��AC��
��1����֤��![]() ��
��![]() ��
��
��2����PCPD��7����AP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ���Գ���Ϊֱ��
���Գ���Ϊֱ��![]() ��ƽ����
��ƽ����![]() ���ֱ���������߽���
���ֱ���������߽���![]() ��
��![]() ���㣬��
���㣬��![]() �ڶԳ�����࣬
�ڶԳ�����࣬![]() .
.
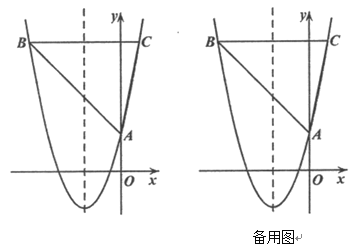
I.��������ߵĽ���ʽ��
��.��֪��![]() ���ϴ���һ��
���ϴ���һ��![]() ��ʹ��
��ʹ��![]() ���ܳ���С�����
���ܳ���С�����![]() �����ꣻ
�����ꣻ
��.������![]() ��ֱ��
��ֱ��![]() ��
��![]() ������ֳ�2:3�����֣�����ֱ��
������ֳ�2:3�����֣�����ֱ��![]() �Ľ���ʽ.
�Ľ���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
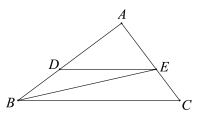
����Ŀ����ͼ����Rt��ABC�У���A=90����AB=8cm��AC=6cm��������D��B���������߶�BA�˶�����AΪֹ��������D��B��A�غϵ���������˶��ٶ�Ϊ2cm/s������D��DE��BC��AC�ڵ�E������BE���趯��D�˶���ʱ��Ϊx��s����AE�ij�Ϊy��cm����
��1����y����x�ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
��2����xΪ��ֵʱ����BDE�����S�����ֵ�����ֵΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ϊ���˽���꼶450��ѧ����������������������˾��꼶����ѧ���������������ԣ���λ�����������ݲ��Խ�����Ƴ������治������ͳ��ͼ����
��� | ������ | Ƶ�� | Ƶ�� |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
��1�������![]() �� ����
�� ����![]() �� ����
�� ����
��2������þ��꼶���������Խ��С��10��������
��3�����������Խ��С��10��Ϊ����꣬��������5������3��������2��Ů�����ִ���5�������ѡ��2�˵��飬��ͨ������״ͼ���б��ķ�����ѡ����2��Ϊһ������һ��Ů���ĸ��ʣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com