
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,平行于
,平行于![]() 轴的直线与抛物线交于
轴的直线与抛物线交于![]() 、
、![]() 两点,点
两点,点![]() 在对称轴左侧,
在对称轴左侧,![]() .
.
I.求此抛物线的解析式;
Ⅱ.已知在![]() 轴上存在一点
轴上存在一点![]() ,使得
,使得![]() 的周长最小,求点
的周长最小,求点![]() 的坐标;
的坐标;
Ⅲ.若过点![]() 的直线
的直线![]() 将
将![]() 的面积分成2:3两部分,试求直线
的面积分成2:3两部分,试求直线![]() 的解析式.
的解析式.
【答案】Ⅰ.![]() ;Ⅱ.点
;Ⅱ.点![]() 的坐标为
的坐标为![]() ;Ⅲ.直线
;Ⅲ.直线![]() 解析式为
解析式为![]() .
.
【解析】
I.由对称轴直线x=2,以及A点坐标确定出b与c的值,即可求出抛物线解析式;
Ⅱ.由抛物线的对称轴及BC的长,确定出B与C的横坐标,代入抛物线解析式求出纵坐标,确定出B与C坐标,再求出点A关于x轴的对称点![]() ,连接
,连接![]() 交x轴于点D,则点D即为所求,利用待定系数法求出
交x轴于点D,则点D即为所求,利用待定系数法求出![]() 的解析式,即可解决问题.
的解析式,即可解决问题.
Ⅲ.利用待定系数法求出直线AB解析式,过Q作QH⊥y轴,与y轴交于点H,BC与y轴交于点M,由已知面积之比求出QH的长,确定出Q横坐标,代入直线AB解析式求出纵坐标,确定出Q坐标,再利用待定系数法求出直线l的解析式.
解:I.由题意得:![]() ,
,![]() ,
,
解得![]() .
.
∴此抛物线的解析式为![]() .
.
Ⅱ.∵抛物线对称轴为直线![]() ,
,![]() ,
,
∴![]() 横坐标为
横坐标为![]() ,
,![]() 横坐标为1.
横坐标为1.
把![]() 代入抛物线解析式得:
代入抛物线解析式得:![]() ,
,
∴![]() ,
,![]() .
.
如图![]() ,点
,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,
,
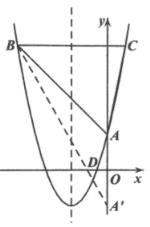
图![]()
设直线![]() 解析式为
解析式为![]() ,
,
把![]() 坐标代入得:
坐标代入得:![]() ,即
,即![]() .
.
令![]() ,解得
,解得![]() ,即点
,即点![]() 的坐标为
的坐标为![]() .
.
Ⅲ.如图![]() ,设直线
,设直线![]() 解析式为
解析式为![]() ,
,
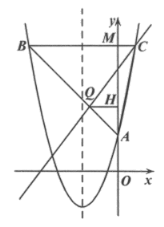
图b
把![]() 坐标代入得
坐标代入得![]() ,即
,即![]() .
.
设直线![]() 与
与![]() 交于点
交于点![]() ,过
,过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,设
,设![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
可得![]() .
.
∴![]() .
.
∵直线![]() 将
将![]() 面积分成2:3两部分,
面积分成2:3两部分,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() 或
或![]() .
.
当![]() 时,把
时,把![]() 代入直线
代入直线![]() 解析式得
解析式得![]() ,
,
此时![]() ,直线
,直线![]() 解析式为
解析式为![]() .
.
当![]() 时,把
时,把![]() 代入直线
代入直线![]() 解析式得
解析式得![]() ,
,
此时![]() ,直线
,直线![]() 解析式为
解析式为![]() .
.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作FG⊥AC于点F,交AB的延长线于点G.
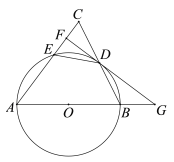
(1)求证:GD为⊙O切线;
(2)求证:DE2=EF·AC;
(3)若tan∠C=2,AB=5,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷两次,记第一次掷出的点数为![]() ,第二次掷出的点数为
,第二次掷出的点数为![]() ,则使关于
,则使关于![]() 的方程组
的方程组![]() 只有正数解的概率为( ).
只有正数解的概率为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=9,S△ABC=![]() ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
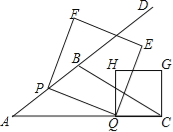
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
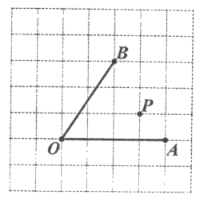
【题目】如图,在每个小正方形的边长为1的网格中,点![]() 、
、![]() 、
、![]() 、
、![]() 均在格点上.I.
均在格点上.I. ![]() 的长等于______________;Ⅱ.点
的长等于______________;Ⅱ.点![]() 在射线
在射线![]() 上,点
上,点![]() 在射线
在射线![]() 上,当
上,当![]() 的周长最小时,请在如图所示的网格中,用无刻度的直尺,画出
的周长最小时,请在如图所示的网格中,用无刻度的直尺,画出![]() ,并简要说明点
,并简要说明点![]() ,
,![]() 的位置是如何找到的(不要求证明)____________ .
的位置是如何找到的(不要求证明)____________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
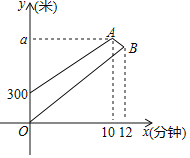
【题目】小明放学后从学校回家,出发![]() 分钟时,同桌小强发现小明的数学作业卷忘记拿了,立即拿着数学作业卷按照同样的路线去追赶小明,小强出发
分钟时,同桌小强发现小明的数学作业卷忘记拿了,立即拿着数学作业卷按照同样的路线去追赶小明,小强出发![]() 分钟时,小明才想起没拿数学作业卷,马上以原速原路返回,在途中与小强相遇.两人离学校的路程
分钟时,小明才想起没拿数学作业卷,马上以原速原路返回,在途中与小强相遇.两人离学校的路程![]() (米)与小强所用时间
(米)与小强所用时间![]() (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.
(1)求函数图象中![]() 的值;
的值;
(2)求小强的速度;
(3)求线段![]() 的函数解析式,并写出自变量的取值范围.
的函数解析式,并写出自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
组别 | 体重(千克) | 人数 |
A | 37.5≤x<42.5 | 10 |
B | 42.5≤x<47.5 | n |
C | 47.5≤x<52.5 | 40 |
D | 52.5≤x<57.5 | 20 |
E | 57.5≤x<62.5 | 10 |

请根据图表信息回答下列问题:
(1)填空:①m=_____,②n=_____,③在扇形统计图中,C组所在扇形的圆心角的度数等于_______度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
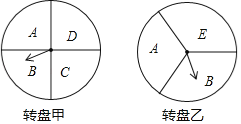
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受9折优惠的概率为 ;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com