
【题目】已知Rt△ABC,AB=3,BC=4,CA=5,P为△ABC外接圆上的一动点,且 ![]() 的最大值是( )
的最大值是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:以AC的中点为原点,以ACx轴,建立如图所示的平面直角坐标系,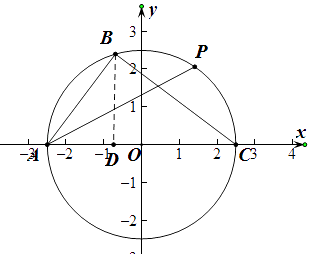
则△ABC外接圆的方程为x2+y2=2.52 ,
设P的坐标为( ![]() cosθ,
cosθ, ![]() sinθ),
sinθ),
过点B作BD垂直x轴,
∵sinA= ![]() ,AB=3
,AB=3
∴BD=ABsinA= ![]() ,AD=ABcosA=
,AD=ABcosA= ![]() ×3=
×3= ![]() ,
,
∴OD=AO﹣AD=2.5﹣ ![]() =
= ![]() ,
,
∴B(﹣ ![]() ,
, ![]() ),
),
∵A(﹣ ![]() ,0),C(
,0),C( ![]() ,0)
,0)
∴ ![]() =(
=( ![]() ,
, ![]() ),
), ![]() =(5,0),
=(5,0), ![]() =(
=( ![]() cosθ+
cosθ+ ![]() ,
, ![]() sinθ)
sinθ)
∵ ![]() =x
=x ![]() +y
+y ![]()
∴( ![]() cosθ+
cosθ+ ![]() ,
, ![]() sinθ)=x(
sinθ)=x( ![]() ,
, ![]() )+y(5,0)=(
)+y(5,0)=( ![]() x+5y,
x+5y, ![]() x)
x)
∴ ![]() cosθ+
cosθ+ ![]() =
= ![]() x+5y,
x+5y, ![]() sinθ=
sinθ= ![]() x,
x,
∴y= ![]() cosθ﹣
cosθ﹣ ![]() sinθ+
sinθ+ ![]() ,x=
,x= ![]() sinθ,
sinθ,
∴x+y= ![]() cosθ+
cosθ+ ![]() sinθ+
sinθ+ ![]() =
= ![]() sin(θ+φ)+
sin(θ+φ)+ ![]() ,其中sinφ=
,其中sinφ= ![]() ,cosφ=
,cosφ= ![]() ,
,
当sin(θ+φ)=1时,x+y有最大值,最大值为 ![]() +
+ ![]() =
= ![]() ,
,
故选:B
【考点精析】解答此题的关键在于理解平面向量的基本定理及其意义的相关知识,掌握如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() .
.


科目:初中数学 来源: 题型:
【题目】已知f(x)=|x﹣a|,a∈R.
(1)当a=1时,求不等式f(x)+|2x﹣5|≥6的解集;
(2)若函数g(x)=f(x)﹣|x﹣3|的值域为A,且[﹣1,2]A,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若存在正实数m,使得关于x的方程x+a(2x+2m﹣4ex)[ln(x+m)﹣lnx]=0成立,其中e为自然对数的底数,则实数a的取值范围是( )
A.(﹣∞,0)
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,已知|AB|=|AC|=1,∠A=120°,E,F分别是AB,AC上的点,且 ![]() ,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则
,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则 ![]() 的最小值为 .
的最小值为 . 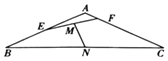
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知曲线C1的参数方程为 ![]() (t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为 ![]() . (I)求曲线C2的直角坐标系方程;
. (I)求曲线C2的直角坐标系方程;
(II)设M1是曲线C1上的点,M2是曲线C2上的点,求|M1M2|的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏从![]() 地出发向
地出发向![]() 地行走,同时小聪从
地行走,同时小聪从![]() 地出发向
地出发向![]() 地行走,如图所示,相交于点
地行走,如图所示,相交于点![]() 的两条线段
的两条线段![]() 分别表示小敏、小聪离
分别表示小敏、小聪离![]() 地的距离
地的距离![]() (km)与已用时间
(km)与已用时间![]() (h)之间的关系,则
(h)之间的关系,则![]() ________时,小敏、小聪两人相距7 km.
________时,小敏、小聪两人相距7 km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABO在平面直角坐标系中,点A(4 ![]() ,0),函数y=
,0),函数y= ![]() (x>0,k为常数)的图象经过AB的中点D,交OB于E.
(x>0,k为常数)的图象经过AB的中点D,交OB于E. 
(1)求k的值;
(2)若第一象限的双曲线y= ![]() 与△BDE没有交点,请直接写出m的取值范围.
与△BDE没有交点,请直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com