
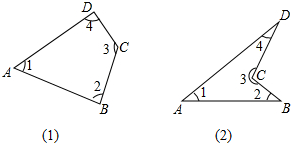
 求图(1)和图(2)中的∠1+∠2+∠3+∠4的度数.
求图(1)和图(2)中的∠1+∠2+∠3+∠4的度数.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
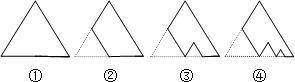
| A. | ${({\frac{1}{4}})^n}$ | B. | ${({\frac{1}{4}})^{n-1}}$ | C. | ${({\frac{1}{2}})^n}$ | D. | ${({\frac{1}{2}})^{n-1}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
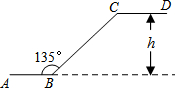 如图是石景山当代商场地下广场到地面广场的手扶电梯示意图.其中AB、CD分别表示地下广场、地面广场电梯口处的水平线.已知∠ABC=135°,BC的长约是$6\sqrt{2}$m,则乘电梯从点B到点C上升的高度h是6m.
如图是石景山当代商场地下广场到地面广场的手扶电梯示意图.其中AB、CD分别表示地下广场、地面广场电梯口处的水平线.已知∠ABC=135°,BC的长约是$6\sqrt{2}$m,则乘电梯从点B到点C上升的高度h是6m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
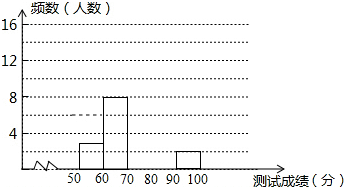 为了增强学生环保意识,我区举办了首届“环保知识大赛”,经选拔后有30名学生参加决赛,这30,名学生同事解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了增强学生环保意识,我区举办了首届“环保知识大赛”,经选拔后有30名学生参加决赛,这30,名学生同事解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 3 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 13 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com