【题目】已知抛物线y＝ax2＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．
(1)求抛物线的函数关系式；
(2)设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；
【答案】（1）抛物线的解析式为：y=-x2+2x+3；(2) P点的坐标为（1,2）.
【解析】
试题（1）根据函数图象经过的三点，用待定系数法确定二次函数的解析式即可；
（2）根据AC是定值，得到当PA+PC最小时，△PAC的周长最小，A点关于直线L的对称点为点B，连接BC交直线L与点P即可得.
试题解析：（1）将三点坐标分别代入解析式，解方程组得：a=-1 b=2 c=3，∴抛物线的解析式为：y=-x2+2x+3；
(2) ∵AC长为定值，∴当PA+PC值为最小时，△PAC的周长最小.
A点关于直线L的对称点为点B，连接BC交直线L与点P，P点的横坐标为1，
直线BC的解析式为：y=-x+3
∴当x=1时，y=2，∴P点的坐标为（1,2）.
科目：初中数学 来源： 题型：
【题目】下列说法正确的是( )
A.为了解全国中学生视力的情况，应采用普查的方式
B.某种彩票中奖的概率是
，买1000张这种彩票一定会中奖
C.从2000名学生中随机抽取200名学生进行调查，样本容量为200名学生
D.从只装有白球和绿球的袋中任意摸出一个球，摸出黑球是确定事件
查看答案和解析>>
科目：初中数学 来源： 题型：
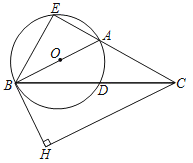
【题目】如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D．延长CA交⊙O于点E，BH是⊙O的切线，作CH⊥BH．垂足为H．
（1）求证：BE＝BH；
（2）若AB＝5，tan∠CBE＝2，求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（9分）在如图的方格中，△OAB的顶点坐标分别为O（0，0）、A（﹣2，﹣1）、B（﹣1，﹣3），△O1A1B1与△OAB是关于点P为位似中心的位似图形．
（1）在图中标出位似中心P的位置，并写出点的坐标及△O1A1B1与△OAB的相似比；
（2）以原点O为位似中心，在y轴的左侧画出△OAB的一个位似△OA2B2，使它与△OAB的位似比为2：1，并写出点B的对应点B2的坐标；
（3）在（2）条件下，若点M（a，b）是△OAB边上一点（不与顶点重合），写出M在△OA2B2中的对应点M2的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知直线
分别为x轴，y轴相交于A，B两点，点P(0，m)是y轴上一个动点，若以点P为圆心的圆P与x轴和直线l都相切，则m的值是_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两车分别从A、B两地同时出发，在同一条公路上，匀速行驶，相向而行，到两车相遇时停止.甲车行驶一段时间后，因故停车0.5小时，故障解除后，继续以原速向B地行驶，两车之间的路程y（千米）与出发后所用时间x(小时）之间的函数关系如图所示.
（1）求甲、乙两车行驶的速度V甲、V乙.
（2）求m的值.
（3）若甲车没有故障停车，求可以提前多长时间两车相遇.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对某一个函数给出如下定义：对于函数y，若当
，函数值y满足
，且满足
，则称此函数为“k属和合函数”
例如：正比例函数
，当
时，
，则
，求得：
，所以函数为“3属和合函数”.
（1）①一次函数
为“k属和合函数”，则k的值为______，
②若一次函数
为“1属和合函数”，求a的值；
（2）反比例函数
（
，且
）是“k属和合函数”，且
，请求出
的值；
（3）已知二次函数
，当
时，y是“k属和合函数”，求k的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
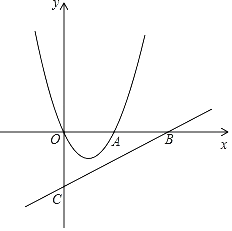
【题目】如图，在平面直角坐标系xOy中，抛物线y＝x2+bx经过点A（2，0）．直线y＝
x﹣2与x轴交于点B，与y轴交于点C．
（1）求这条抛物线的表达式和顶点的坐标；
（2）将抛物线y＝x2+bx向右平移，使平移后的抛物线经过点B，求平移后抛物线的表达式；
（3）将抛物线y＝x2+bx向下平移，使平移后的抛物线交y轴于点D，交线段BC于点P、Q，（点P在点Q右侧），平移后抛物线的顶点为M，如果DP∥x轴，求∠MCP的正弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
