
����Ŀ����ijһ�������������¶��壺���ں���y������![]() ������ֵy����
������ֵy����![]() ��������
��������![]() ����ƴ˺���Ϊ��k���ͺϺ�����
����ƴ˺���Ϊ��k���ͺϺ�����
���磺����������![]() ����
����![]() ʱ��
ʱ��![]() ����
����![]() ����ã�
����ã�![]() �����Ժ���
�����Ժ���![]() Ϊ��3���ͺϺ�����.
Ϊ��3���ͺϺ�����.
��1����һ�κ���![]() Ϊ��k���ͺϺ���������k��ֵΪ______��
Ϊ��k���ͺϺ���������k��ֵΪ______��
����һ�κ���![]() Ϊ��1���ͺϺ���������a��ֵ��
Ϊ��1���ͺϺ���������a��ֵ��
��2������������![]() ��
��![]() ��
��![]() ��
��![]() ���ǡ�k���ͺϺ���������
���ǡ�k���ͺϺ���������![]() �������
�������![]() ��ֵ��
��ֵ��
��3����֪���κ���![]() ����
����![]() ʱ��y�ǡ�k���ͺϺ���������k��ȡֵ��Χ.
ʱ��y�ǡ�k���ͺϺ���������k��ȡֵ��Χ.
���𰸡���1����2����![]() ����2��2018����3����a��1ʱ��
����2��2018����3����a��1ʱ��![]() ����0��a��1ʱ��
����0��a��1ʱ��![]() ������1��a��0ʱ��
������1��a��0ʱ��![]() ����a����1ʱ��
����a����1ʱ��![]() .
.
��������
��1���ٸ�����k���ͺϺ������Ķ��弴�����k��ֵ��
�ڸ���a��ȡֵ��Χ�������ۣ�Ȼ���ٸ�����1���ͺϺ������Ķ���ֱ���a��ֵ���ɣ�
��2�����ݷ����������������ԣ����y��ȡֵ��Χ��Ȼ�������k���ͺϺ������Ķ��弴�����ab��ֵ��Ȼ��������ȫƽ����ʽ�ı��μ������![]() ��ֵ��
��ֵ��
��3�����ݶԳ�����x��ȡֵ��Χ�����λ�÷������ۣ���i����a��1ʱ����![]() �ڶԳ�����࣬���ݶ��κ��������������y��ȡֵ��Χ��Ȼ�������k���ͺϺ������Ķ��弴�����k��a�Ĺ�ϵ������a��ȡֵ���k��ȡֵ���ɣ���ii����0��a��1ʱ����
�ڶԳ�����࣬���ݶ��κ��������������y��ȡֵ��Χ��Ȼ�������k���ͺϺ������Ķ��弴�����k��a�Ĺ�ϵ������a��ȡֵ���k��ȡֵ���ɣ���ii����0��a��1ʱ����![]() ���Գ��ᣬ��x=��1��Գ�����Զ��ԭ��ͬ�ϣ���iii������1��a��0ʱ����
���Գ��ᣬ��x=��1��Գ�����Զ��ԭ��ͬ�ϣ���iii������1��a��0ʱ����![]() ���Գ��ᣬ��x=1��Գ�����Զ��ԭ��ͬ�ϣ���iiii����a����1ʱ����
���Գ��ᣬ��x=1��Գ�����Զ��ԭ��ͬ�ϣ���iiii����a����1ʱ����![]() �ڶԳ����Ҳ࣬ԭ��ͬ��.
�ڶԳ����Ҳ࣬ԭ��ͬ��.
�⣺��1���١�һ�κ���![]() ��
��![]() ʱ
ʱ![]() ��
��
������k���ͺϺ������Ķ��壺![]() ��
��
��ã�k=2��
�ڵ�a��0ʱ��
��![]() ��
��![]() ʱ��
ʱ��![]() ��
��
������1���ͺϺ������Ķ��壺![]() ��
��
��ã�![]() ��
��
��a��0ʱ��
��![]() ��
��![]() ʱ��
ʱ��![]() ��
��
������1���ͺϺ������Ķ��壺![]() ��
��
��ã�![]() ��
��
����������![]() ��
��
��2����![]() ��
��![]() ��
��![]() ��
��![]() ����
����
�൱![]() ʱ��y��x���������С��
ʱ��y��x���������С��
��![]() ��
��
������k���ͺϺ������Ķ��壺![]() ��
��
��ã�![]() ��
��
��![]() ��
��
��![]() ��
��
��3�����κ���![]() �ĶԳ���Ϊ��
�ĶԳ���Ϊ��![]() ��
��
��i����a��1ʱ����![]() �ڶԳ�����࣬����ͼ��ʾ��
�ڶԳ�����࣬����ͼ��ʾ��
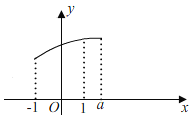
���ѷ��֣���x=1ʱ��y���ֵΪ��![]() ��
��
��x=��1ʱ��y��СֵΪ��![]() ��
��
������k���ͺϺ������Ķ��壺![]() ��
��
��ã�![]() ��
��
��a��1��
��![]() ��
��
��ii����0��a��1ʱ����![]() ���Գ��ᣬ��x=��1��Գ�����Զ������ͼ��ʾ��
���Գ��ᣬ��x=��1��Գ�����Զ������ͼ��ʾ��
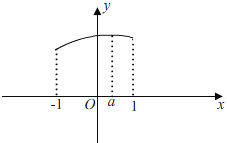
���ѷ��֣���x=aʱ��y���ֵΪ��![]() ��
��
��x=��1ʱ��y��СֵΪ��![]() ��
��
������k���ͺϺ������Ķ��壺![]() ��
��
��ã�![]() ���˺����ĶԳ���Ϊ��a=��1���������ϣ�
���˺����ĶԳ���Ϊ��a=��1���������ϣ�
��0��a��1�ڶԳ�����Ҳ࣬k��a�����������
�൱0��a��1ʱ����ã�![]() ��
��
��iii������1��a��0ʱ����![]() ���Գ��ᣬ��x=1��Գ�����Զ������ͼ��ʾ��
���Գ��ᣬ��x=1��Գ�����Զ������ͼ��ʾ��
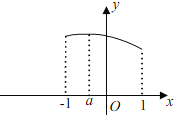
���ѷ��֣���x=aʱ��y���ֵΪ��![]() ��
��
��x=1ʱ��y��СֵΪ��![]() ��
��
������k���ͺϺ������Ķ��壺![]()
��ã�![]() ���˺����ĶԳ���Ϊ��a=1���������ϣ�
���˺����ĶԳ���Ϊ��a=1���������ϣ�
�ੁ1��a��0�ڶԳ������࣬k��a���������С
�൱��1��a��0ʱ����ã�![]() ��
��
��iiii����a����1ʱ����![]() �ڶԳ����Ҳ࣬����ͼ��ʾ��
�ڶԳ����Ҳ࣬����ͼ��ʾ��

���ѷ��֣���x=1ʱ��y��СֵΪ��![]() ��
��
��x=��1ʱ��y���ֵΪ��![]() ��
��
������k���ͺϺ������Ķ��壺![]()
��ã�![]()
��a����1��
��![]() ��
��
������������a��1ʱ��![]() ����0��a��1ʱ��
����0��a��1ʱ��![]() ������1��a��0ʱ��
������1��a��0ʱ��![]() ����a����1ʱ��
����a����1ʱ��![]() .
.


 ̽���빮�̺��Ͽ�ѧ����������ϵ�д�
̽���빮�̺��Ͽ�ѧ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��С�����η���ı߳�Ϊ 1,
��Ҫ����ͼ��������Ҫ�������⣺

��1����ͼ������ͼ��С�����η����ij�������㣬�ֱ�õ������߶�![]() ��
��![]() ��
��![]() ��ʹ��
��ʹ��![]() ��
��![]() ��
��![]() ��
��
��2���жϣ�1���е������߶�![]() ��
��![]() ��
��![]() �ܷ�����������˵������.
�ܷ�����������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2��bx��c����A(��1��0)��B(3��0)��C(0��3)���㣬ֱ��l�������ߵĶԳ��ᣮ

(1)�������ߵĺ�����ϵʽ��
(2)���P��ֱ��l�ϵ�һ�����㣬����PAC���ܳ���Сʱ�����P�����ꣻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O��һ�㣬����O��OD��AB����BC���ӳ�����D����AC�ڵ�E��F��DE���е㣬����CF��
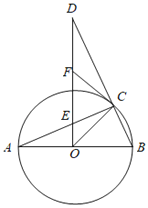
��1����֤��CF�ǡ�O�����ߣ�
��2������A��22.5������֤��AC��DC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
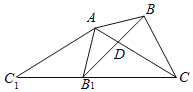
����Ŀ����ͼ����ABC�У���BAC��45������ACB��30��������ABC�Ƶ�A˳ʱ����ת�õ���A1B1C1����C��B1��C1���㹲��ʱ����ת��Ϊ��������BB1������AC�ڵ�D��������ۣ�
�١�AC1CΪ���������Σ���CA��CB1��������135�����ܡ�AB1D�ס�ACB1����![]() ��
��![]() �У���ȷ�Ľ��۵����Ϊ______��
�У���ȷ�Ľ��۵����Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���B��30�㣬AB��AC��O�������Խ��ߵĽ��㣬����O��AC�Ĵ��߷ֱ�AD��BC�ڵ�E��F����M�DZ�AB��һ�����ȷֵ㣮����MF�����AOE���BMF�������Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
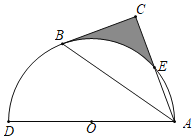
����Ŀ����ͼ����ADΪֱ���İ�ԲO����Rt��ABCб��AB�������˵㣬��ֱ�DZ�AC�ڵ�E��B��E�ǰ�Բ�������ȷֵ㣬![]() �ij�Ϊ
�ij�Ϊ![]() ����ͼ����Ӱ���ֵ����Ϊ��������
����ͼ����Ӱ���ֵ����Ϊ��������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��ijƷ��̨����ֱ�ڷ���ˮƽ�����ϵIJ���ʾ��ͼ������![]() Ϊ���棨̨�Ƶ����ĺ�Ⱥ��Բ��ƣ���̨��֧��
Ϊ���棨̨�Ƶ����ĺ�Ⱥ��Բ��ƣ���̨��֧��![]() ��ƹ�
��ƹ�![]() �ij��ȶ�Ϊ
�ij��ȶ�Ϊ![]() ���Ҽн�Ϊ
���Ҽн�Ϊ![]() ����
����![]() ���������ָüнDz��䣬��֧��
���������ָüнDz��䣬��֧��![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ʱ��֧����ƹ�����
ʱ��֧����ƹ�����![]() λ�ã���ͼ2��ʾ������ƹ�ĩ��
λ�ã���ͼ2��ʾ������ƹ�ĩ��![]() �ĸ߶Ȼή��_______
�ĸ߶Ȼή��_______![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
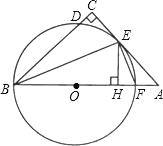
����Ŀ����ͼ������ABC�У���C=90������ABC��ƽ���߽�AC�ڵ�E������E��BE�Ĵ��߽�AB�ڵ�F����O����BEF�����Բ��
��1����֤��AC����O�����ߣ�
��2������E��EH��AB������ΪH����֤��CD=HF��
��3����CD=1��EH=3����BF��AF����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com