【题目】某同学使用计算器求10个数据的平均值时，错将其中一个数据20输入为10，结果得到平均数14，那么由此算出的方差与实际方差的差为________．
【答案】-1
【解析】
利用方差公式，计算方差，即可得出结论．
解：设弄错的数是第10个，设前9个数分别是x1，x2…，x9， 两个方差分别为S1和S2， 则：
S1=
[（x1-14）2+（x2-14）2+…+（x9-14）2+（10-14）2]，
S2= [（x1-15）2+（x2-15）2+…+（x9-15）2+（10-15）2]，
两式相减得：
S1-S2=[（x1-14）2+（x2-14）2+…+（x9-14）2+（10-14）2]-[（x1-15）2+（x2-15）2+…+（x9-15）2+（10-15）2]
= [（x1-14）2-（x1-15）2+（x2-14）2-（x2-15）2+…+（x9-14）2-（x9-15）2+（16-25）]
= [2（x1+x2+…+x9）-29×9-9]
=（2×130-270）=-1．
故答案为：-1．
科目：初中数学 来源： 题型：
【题目】某工厂准备翻建新的大门，厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m，最大高度OC=4m，工厂的运输卡车的高度是3m，宽度是5.8m.现设计了两种方案.方案一：建成抛物线形状（如图1）；方案二：建成圆弧形状（如图2）.为确保工厂的卡车在通过厂门时更安全，你认为应采用哪种设计方案？请说明理由.
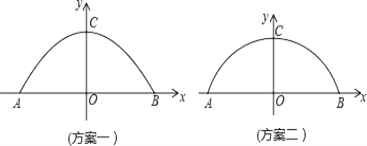
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数y=ax2+bx+c的图象与x轴交于B、C两点，交y轴于点A．
（1）根据图象确定a，b，c的符号；
（2）如果OC=OA=
OB，BC=4，求这个二次函数的解析式．
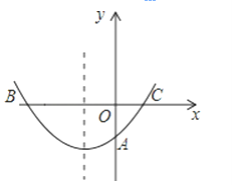
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，小明在山脚下的A处测得山顶N的仰角为45°，此时，他刚好与山底D在同一水平线上．然后沿着坡度为30°的斜坡正对着山顶前行110米到达B处，测得山顶N的仰角为60°．求山的高度．（结果精确到1米，参考数据： 
≈1.414， 
≈1.732）．
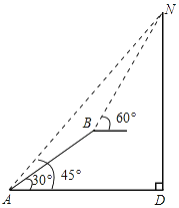
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是由一些棱长为1的小立方块所搭几何体的三种视图．若在所搭几何体的基础上（不改变原几何体中小立方块的位置），继续添加相同的小立方块，以搭成一个长方体，至少还需要________个小立方块．最终搭成的长方体的表面积是________．
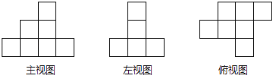
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，O为BD中点，以BC为边向正方形内作等边△BCE,连接并延长AE交CD于F,连接BD分别交CE、AF于G、H,下列结论：①∠CEH=45;②GF∥DE;③2OH+DH=BD;④BG=
DG;⑤
.其中正确的结论是（ ）
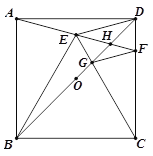
A. ①②③ B. ①②④ C. ①②⑤ D. ②④⑤
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，点F、C是⊙O上两点，且 
= 
=
，连接AC、AF，过点C作CD⊥AF，交AF的延长线于点D，垂足为D，若CD=2
，则⊙O的半径为（ ）
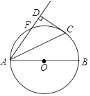
A. 2 B. 4 C. 2 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：
我们知道，四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形相似（不全等），我们就把这条对角线叫做这个四边形的“相似对角线”．
理解：
（1）如图1，已知Rt△ABC在正方形网格中，请你只用无刻度的直尺在网格中找到一点D，使四边形ABCD是以AC为“相似对角线”的四边形（保留画图痕迹，找出3个即可）；
（2）如图2，在四边形ABCD中，∠ABC=80°，∠ADC=140°，对角线BD平分∠ABC．
求证：BD是四边形ABCD的“相似对角线”；
（3）如图3，已知FH是四边形EFCH的“相似对角线”，∠EFH=∠HFG=30°，连接EG，若△EFG的面积为2
，求FH的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
