练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

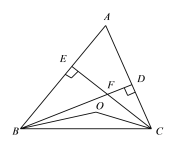
    【题目】如图，已知中，，于D，于E，BD、CE交于点F，、的平分线交于点O，则的度数为____________．

    【答案】

    【解析】

    根据垂直定义可得：∠BEF=∠CDF=90°，然后根据三角形外角的性质，分别求出∠ABD和∠BFC，然后根据三角形的内角和求出∠FBC＋∠FCB，然后根据角平分线的定义和三角形的内角和定理，即可求出.

    解：∵，，

    ∴∠BEF=∠CDF=90°

    ∴∠ABD=∠CDF－∠A=30°

    ∴∠BFC=∠BEF＋∠ABD=120°

    ∴∠FBC＋∠FCB=180°－∠BFC=60°

    ∵、的平分线交于点O

    ∴∠OBC=，∠OCB=

    ∴=180°－（∠OBC＋∠OCB）

    =180°－（＋）

    =180°－（＋）

    =180°－×60°

    =150°

    故答案为：150°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示，正方形ABCD中，E、F分别是BC、DC上的一点，连接AE、AF， AE、AF交于点H且∠AHB=90°.

    （1）求证：BE=CF．

    （2）若正方形面积是25m2，BE=AD，求AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是（　　）

    A.一个三角形的三边长分别为：a，b，c，且a2﹣b2＝c2，则这个三角形是直角三角形

    B.三边长度分别为1，1，的三角形是直角三角形，且1，1，是组勾股数

    C.三边长度分别是12，35，36的三角形是直角三角形

    D.在一个直角三角形中，有两边的长度分别是3和5，则另一边的长度一定是4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠A＝∠B＝90°，E是AB上的一点，且AE＝BC，∠1＝∠2．

    求证：△CED是等腰直角三角形

    证明：∵∠1＝∠2（　 　）

    ∴EC＝　 　（在一个三角形中，等角对等边）

    ∵∠A＝∠B＝90°，AE＝BC

    ∴△AED≌△BCE（　 　）

    ∴∠AED＝∠　 　（　 　）

    ∵∠BCE+∠BEC＝90°

    ∠　 　+∠BEC＝90°（等量代换）

    ∴∠DEC＝90°．

    ∴△CED是等腰直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知.

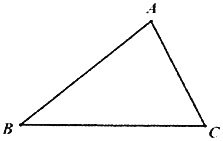
    （1）根据要求作图：在边上求作一点，使得点到、的距离相等，在边上求作一点，使得点到点、的距离相等；（不需要写作法，但需要保留作图痕迹和结论）

    （2）在第（1）小题所作出的图中，求证：.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道：x2﹣6x＝(x2﹣6x+9)﹣9＝(x﹣3)2﹣9；﹣x2+10＝﹣(x2﹣10x+25)+25＝﹣(x﹣5)2+25，这一种方法称为配方法，利用配方法请解以下各题：

    (1)按上面材料提示的方法填空：a2﹣4a＝　 　＝　 　．﹣a2+12a＝　 　＝　 　．

    (2)探究：当a取不同的实数时在得到的代数式a2﹣4a的值中是否存在最小值？请说明理由．

    (3)应用：如图．已知线段AB＝6，M是AB上的一个动点，设AM＝x，以AM为一边作正方形AMND，再以MB、MN为一组邻边作长方形MBCN．问：当点M在AB上运动时，长方形MBCN的面积是否存在最大值？若存在，请求出这个最大值；否则请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】当三角形中一个内角是另一个内角的2倍时，则称此三角形为“倍角三角形”，其中角称为“倍角”.若“倍角三角形”中有一个内角为36°，则这个“倍角三角形”的“倍角”的度数可以是________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，己知直线过与交于点、点，与交于点，直线与轴交于点，且，则________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形中，为对角线，为上一点，连接，，的延长线交于点，，则的度数为________．

    查看答案和解析>>

    同步练习册答案