
【题目】如图,在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:①△AED≌△DFB; ②S四边形BCDG=![]() CG2;③DE=CG;④若AF=2DF,则BG=6GF.其中正确的结论_____________.
CG2;③DE=CG;④若AF=2DF,则BG=6GF.其中正确的结论_____________.

【答案】1 2 4
【解析】分析:(1)由已知条件易得∠A=∠BDF=60°,结合BD=AB=AD,AE=DF,即可证得△AED≌△DFB,从而说明结论①正确;(2)由已知条件可证点B、C、D、G四点共圆,从而可得∠CDN=∠CBM,如图,过点C作CM⊥BF于点M,过点C作CN⊥ED于点N,结合CB=CD即可证得△CBM≌△CDN,由此可得S四边形BCDG=S四边形CMGN=2S△CGN,在Rt△CGN中,由∠CGN=∠DBC=60°,∠CNG=90°可得GN=![]() CG,CN=
CG,CN=![]() CG,由此即可求得S△CGN=
CG,由此即可求得S△CGN=![]() CG2,从而可得结论②是正确的;(3)由已知易得△ADE中,∠AED>∠A=60°,从而可得AD>DE;在△DCG中,∠CDG>∠CGD=60°,从而可得CG>DC;结合AD=CD即可得到CG>DE,从而说明结论③错误;(4)过点F作FK∥AB交DE于点K,由此可得△DFK∽△DAE,△GFK∽△GBE,结合AF=2DF和相似三角形的性质即可证得结论④成立.
CG2,从而可得结论②是正确的;(3)由已知易得△ADE中,∠AED>∠A=60°,从而可得AD>DE;在△DCG中,∠CDG>∠CGD=60°,从而可得CG>DC;结合AD=CD即可得到CG>DE,从而说明结论③错误;(4)过点F作FK∥AB交DE于点K,由此可得△DFK∽△DAE,△GFK∽△GBE,结合AF=2DF和相似三角形的性质即可证得结论④成立.
详解:
(1)∵四边形ABCD是菱形,BD=AB,
∴AB=BD=BC=DC=DA,
∴△ABD和△CBD都是等边三角形,
∴∠A=∠BDF=60°,
又∵AE=DF,
∴△AED≌△DFB,即结论①正确;
(2)∵△AED≌△DFB,△ABD和△DBC是等边三角形,
∴∠ADE=∠DBF,∠DBC=∠CDB=∠BDA=60°,
∴∠GBC+∠CDG=∠DBF+∠DBC+∠CDB+∠GDB=∠DBC+∠CDB+∠GDB+∠ADE=∠DBC+∠CDB+∠BDA=180°,
∴点B、C、D、G四点共圆,
∴∠CDN=∠CBM,
如下图,过点C作CM⊥BF于点M,过点C作CN⊥ED于点N,
∴∠CDN=∠CBM=90°,
又∵CB=CD,
∴△CBM≌△CDN,
∴S四边形BCDG=S四边形CMGN=2S△CGN,
∵在Rt△CGN中,∠CGN=∠DBC=60°,∠CNG=90°
∴GN=![]() CG,CN=
CG,CN=![]() CG,
CG,
∴S△CGN=![]() CG2,
CG2,
∴S四边形BCDG=2S△CGN,=![]() CG2,即结论②是正确的;
CG2,即结论②是正确的;
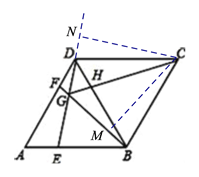
(3)∵在△ABD是等边三角形,
∴∠A=60°,∠AED>∠ABD=60°,
∴∠AED>∠A,
∴DE<AD,
同理,在△DGC中:∠GDC>∠DGC,
∴CG>CD,
∵AD=CD,
∴DE<CG,即结论③错误;
(4)如下图,过点F作FK∥AB交DE于点K,
∴△DFK∽△DAE,△GFK∽△GBE,
∴![]() ,
,![]() ,
,
∵AF=2DF,
∴![]() ,
,
∵AB=AD,AE=DF,AF=2DF,
∴BE=2AE,
∴![]() ,
,
∴BG=6FG,即结论④成立.
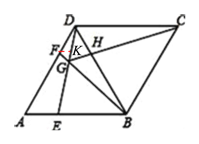
综上所述,本题中正确的结论是:
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】(1)请画出△ABC关于y轴对称的△A'B'C'(其中A',B',C'分别是A,B,C的对应点,不写画法).
(2)直接写出A′,B′,C'三点的坐标:A'_______,B'______,C'______;
(3)△ABC的面积为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.

(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)共抽取了多少个学生进行调查?
(2)将图甲中的折线统计图补充完整.
(3)求出图乙中B等级所占圆心角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,等腰Rt△OAB中,∠AOB=90°,等腰Rt△EOF中,∠EOF=90°,连结AE、BF.

求证:(1)AE=BF;(2)AE⊥BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高空的气温与距地面的高度有关,某地距地面的高度每升高1km,气温下降6℃,已知地面气温为20℃.
(1)写出该地空中气温T(℃)与高度h(km)之间的函数表达式.
(2)求距离地面上4km处的气温T.
(3)求气温为-16℃处距地面的高度h.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
(3)点P(a+1,b-1)与点C关于x轴对称,则a= ,b= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 的图象经过点(﹣1,﹣2
的图象经过点(﹣1,﹣2![]() ),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当
),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当![]() 时,则点C的坐标为______.
时,则点C的坐标为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com