
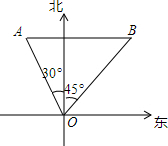
 如图,某海防哨所(O)发现在它的北偏西30°,距离为500m的A处有一艘船,该船向正东方向航行,经过3min到达哨所东北方向的B处,则该船的航速为每小时13.7km.(精确到0.1)
如图,某海防哨所(O)发现在它的北偏西30°,距离为500m的A处有一艘船,该船向正东方向航行,经过3min到达哨所东北方向的B处,则该船的航速为每小时13.7km.(精确到0.1) 分析 设AB与正北方向线交于点C,根据已知及三角函数求得AC、OC的长,再根据等腰直角三角形的性质求得BC的长,利用AB=AC+BC求出AB的长,再除以该船航行的时间即可求解.
解答 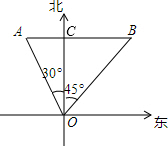 解:设AB与正北方向线交于点C,
解:设AB与正北方向线交于点C,
∵在直角△AOC中,∠AOC=30°,OA=500米,
∴AC=OA•sin30°=250米,OC=OA•cos30°=250$\sqrt{3}$米,
∵直角△OBC是等腰直角三角形,
∴BC=OC=250$\sqrt{3}$米,
∴AB=AC+BC=250+250$\sqrt{3}$(米),
∴该船的航速为$\frac{250+250\sqrt{3}}{1000}$÷$\frac{3}{60}$=5+5$\sqrt{3}$≈13.7(千米/时),
即该船的航速约为每小时13.7千米.
故答案为13.7.
点评 本题考查了解直角三角形的知识,解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法构造直角三角形,难度一般.


科目:初中数学 来源: 题型:选择题
| A. | 由有一个公共端点且相等的两条线段组成的图形一定是轴对称图形 | |
| B. | 由有一个公共端点且不相等的两条线段组成的图形一定不是轴对称图形 | |
| C. | 锐角三角形一定是轴对称图形 | |
| D. | 锐角三角形一定不是轴对称图形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
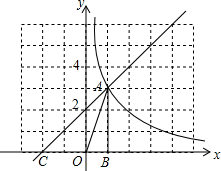 如图,在平面直角坐标系中,直线y=x+$\frac{1}{2}m$的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限内交于点A,与x轴交于点C,AB垂直于X轴,垂足为B,且三角形AOB的面积为1.
如图,在平面直角坐标系中,直线y=x+$\frac{1}{2}m$的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限内交于点A,与x轴交于点C,AB垂直于X轴,垂足为B,且三角形AOB的面积为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
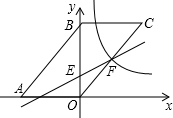 如图,在平面直角坐标系中,四边形ABCO是平行四边形,A点坐标(-6,0),B点坐标(0,6),点C在第一象限,直线y=$\frac{1}{2}$x+2与y轴交与点E,与OC交与点F,反比例函数y=$\frac{k}{x}$(x>0)经过点F.
如图,在平面直角坐标系中,四边形ABCO是平行四边形,A点坐标(-6,0),B点坐标(0,6),点C在第一象限,直线y=$\frac{1}{2}$x+2与y轴交与点E,与OC交与点F,反比例函数y=$\frac{k}{x}$(x>0)经过点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
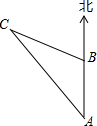 如图,上午8时,一艘轮船从A处出发以每小时20海里的速度向正北航行,10时到达B处,则轮船在A处测得灯塔C在北偏西36°,航行到B处时,又测得灯塔C在北偏西72°,则从B到灯塔C的距离是40海里.
如图,上午8时,一艘轮船从A处出发以每小时20海里的速度向正北航行,10时到达B处,则轮船在A处测得灯塔C在北偏西36°,航行到B处时,又测得灯塔C在北偏西72°,则从B到灯塔C的距离是40海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com