
【题目】如下图所示,直线y=-![]() x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
(1)求出点C的坐标;
(2)若△OQC是等腰直角三角形,则t的值为________;
(3)若CQ平分△OAC的面积,求直线CQ对应的函数表达式.

【答案】(1)点C的坐标为(2,2);(2)t的值为2或4;(3)直线CQ对应的函数表达式为y=-2x+6.
【解析】
(1)以![]() 和
和![]() 组成二元一次方程组,解此方程组即可求得点C的坐标;
组成二元一次方程组,解此方程组即可求得点C的坐标;
(2)由题意可知,∠COQ是锐角,由此可得若△COQ是等腰直角三角形,存在以下两种情况:①∠CQO=90°;②∠OCQ=90°;根据两种情况画出图形,结合已知条件分析解答即可求得对应的t的值;
(3)由题意可知,当点Q是线段OA的中点时,CQ平分△OCA的面积,由此结合已知条件求得点线段OA的中点的坐标即可求得此时CQ的解析式了.
(1)由 解得:
解得:![]() ,
,
∴点C的坐标为(2,2).
(2) 由题意可知,∠COQ是锐角,由此可得若△COQ是等腰直角三角形,存在以下两种情况:①∠CQO=90°;②∠OCQ=90°;先分别解答如下:
I、如图①,当∠CQO=90°,CQ=OQ时,
∵C(2,2),
∴OQ=CQ=2,解得:t=2;

II、如图②,当∠OCQ=90°,OC=CQ时,过点C作CM⊥OA于点M,
∵C(2,2),
∴CM=OM=2,
∴QM=OM=2,
∴OQ=4,
∴t=4.
综上所述,若△OCQ是等腰直角三角形,则t的值为2或4.
(3)令-![]() x+3=0,得x=6,
x+3=0,得x=6,
∴A(6,0).
∴点Q的坐标为(3,0)时,CQ平分△OCA的面积.
设直线CQ的函数表达式为y=kx+b.
把C(2,2),Q(3,0)代入y=kx+b得:
![]() ,
,
解得k=-2,b=6,
∴当直线CQ平分△OCA的面积时,其对应的函数表达式为y=-2x+6.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
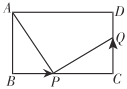
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,设点
运动,设点![]() 的运动时间为
的运动时间为![]() 秒,且
秒,且![]() .
.

(1)![]() _________
_________![]() (用含
(用含![]() 的代数式表示).
的代数式表示).
(2)如图,当点![]() 从点
从点![]() 开始运动的同时,点
开始运动的同时,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,是否存在这样的
运动,是否存在这样的![]() 值,使得以
值,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与以
为顶点的三角形与以![]() 、
、![]() 、
、![]() 为顶点的三角形全等?若存在,请求出v的值;若不存在,请说明理由.
为顶点的三角形全等?若存在,请求出v的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点B(7,6),顶点A、C在坐标轴上,矩形内部一点D在双曲线y=![]() 上,DE⊥AB于点E,DF⊥BC于点F,若四边形DEBF为正方形,则点D的坐标是( )
上,DE⊥AB于点E,DF⊥BC于点F,若四边形DEBF为正方形,则点D的坐标是( )

A. (2,6) B. (3,4) C. (4,3) D. (6,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是【 】

(A)汽车在高速公路上的行驶速度为100km/h
(B)乡村公路总长为90km
(C)汽车在乡村公路上的行驶速度为60km/h
(D)该记者在出发后4.5h到达采访地
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:直线y=x与反比例函数y=![]() (k>0)的图象在第一象限内交于点A(2,m).
(k>0)的图象在第一象限内交于点A(2,m).
(1)求m、k的值;
(2)点B在y轴负半轴上,若△AOB的面积为2,求AB所在直线的函数表达式;
(3)将△AOB沿直线AB向上平移,平移后A、O、B的对应点分别为A'、O'、B',当点O'恰好落在反比例函数y=![]() 的图象上时,求点A'的坐标.
的图象上时,求点A'的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
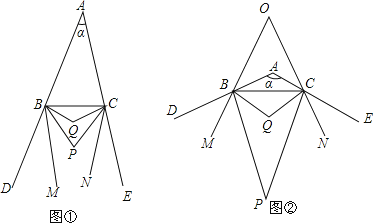
【题目】已知如图①,BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,BQ、CQ分别是∠PBC、∠PCB的角平分线,BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α.
(1)当α=40°时,∠BPC= °,∠BQC= °;
(2)当α= °时,BM∥CN;
(3)如图②,当α=120°时,BM、CN所在直线交于点O,求∠BOC的度数;
(4)在α>60°的条件下,直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像经过A(0,3),(
的图像经过A(0,3),(![]() ,
,![]() )两点.
)两点.
(1)求b、c的值.
(2)二次函数![]() 的图像与
的图像与![]() 轴是否有公共点?若有,求公共点的坐标,若没有,请说明情况.
轴是否有公共点?若有,求公共点的坐标,若没有,请说明情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com