
����Ŀ����֪��ͼ����BP��CP�ֱ��ǡ�ABC����ǡ�CBD����BCE�Ľ�ƽ���ߣ�BQ��CQ�ֱ��ǡ�PBC����PCB�Ľ�ƽ���ߣ�BM��CN�ֱ��ǡ�PBD����PCE�Ľ�ƽ���ߣ���BAC������
��1��������40��ʱ����BPC���� ���㣬��BQC���� ���㣻
��2���������� ����ʱ��BM��CN��
��3����ͼ����������120��ʱ��BM��CN����ֱ�߽��ڵ�O�����BOC�Ķ�����
��4��������60��������£�ֱ��д����BPC����BQC����BOC����֮���������ϵ���� ����
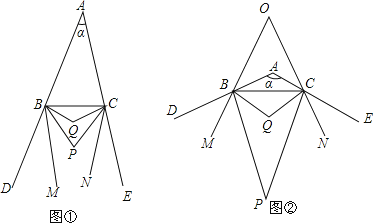
���𰸡���1��70�� 125����2��60����3��45�㣻��4����BPC+��BQC+��BOC��180�㣮
��������
��1�����������ε�������ʷֱ��ʾ����DBC���BCE���ٸ��ݽ�ƽ���ߵ����ʿ���á�CBP+��BCP���������������ڽǺͶ���������⣻���ݽ�ƽ���ߵĶ���ó���QBC��![]() ��PBC����QCB��
��PBC����QCB��![]() ��PCB�������QBC+��QCB�Ķ����������������ڽǺͶ���������ɣ�
��PCB�������QBC+��QCB�Ķ����������������ڽǺͶ���������ɣ�
��2������ƽ���ߵ����ʵõ���MBC+��NCB��180�㣬������⼴�ɣ�
��3����������õ���MBC+��NCB���ٸ�����������ǵ����ʺ��������ڽǺͶ����õ���BOC�Ķ�����
��4���ֱ��á�A��ʾ����BPC����BQC����BOC������Ӽ�����⣮
�⣺��1���ߡ�DBC����A+��ACB����BCE����A+��ABC��
���DBC+��BCE��180��+��A��220�㣬
��BP��CP�ֱ��ǡ�ABC����ǡ�CBD����BCE�Ľ�ƽ���ߣ�
���CBP+��BCP��![]() ����DBC+��BCE����110�㣬
����DBC+��BCE����110�㣬
���BPC��180�㩁110�㣽70�㣬
��BQ��CQ�ֱ��ǡ�PBC����PCB�Ľ�ƽ���ߣ�
���QBC��![]() ��PBC����QCB��
��PBC����QCB��![]() ��PCB��
��PCB��
���QBC+��QCB��55�㣬
���BQC��180�㩁55�㣽125�㣻
��2����BM��CN��
���MBC+��NCB��180�㣬
��BM��CN�ֱ��ǡ�PBD����PCE�Ľ�ƽ���ߣ���BAC������
��![]() ����DBC+��BCE����180�㣬
����DBC+��BCE����180�㣬
��![]() ��180��+������180�㣬
��180��+������180�㣬
�������60�㣻
��3��������120�㣬
���MBC+��NCB��![]() ����DBC+��BCE����
����DBC+��BCE����![]() ��180��+������225�㣬
��180��+������225�㣬
���BOC��225�㩁180�㣽45�㣻
��4��������60�㣬
��BPC��90�㩁![]() ��
��
��BQC��135�㩁![]() ��
��
��BOC��![]() ����45�㣮
����45�㣮
��BPC����BQC����BOC����֮���������ϵ����BPC+��BQC+��BOC����90�㩁![]() ����+��135�㩁
����+��135�㩁![]() ����+��
����+��![]() ����45�㣩��180�㣮
����45�㣩��180�㣮
�ʴ�Ϊ��70��125��60����BPC+��BQC+��BOC��180�㣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �ķ���
�ķ���![]() .
.
��1����֤����������ʵ������2�������̵ĸ�Ϊ��������������![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��֪a��b��7��ab��10����a2��b2��(a��b)2��ֵ��
(2)�Ȼ���(![]() -
-![]() )��
)��![]() �����ش�ԭ����ʽ��ֵ���Ե��ڣ�1��Ϊʲô��
�����ش�ԭ����ʽ��ֵ���Ե��ڣ�1��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ��ֱ��y����![]() x��3��������ֱ��ڵ�A��B����ֱ��y��x���ڵ�C���߶�OA�ϵĵ�Q��ÿ��1����λ���ٶȴӵ�O�������A�������˶����˶�ʱ��Ϊt�룬����CQ.
x��3��������ֱ��ڵ�A��B����ֱ��y��x���ڵ�C���߶�OA�ϵĵ�Q��ÿ��1����λ���ٶȴӵ�O�������A�������˶����˶�ʱ��Ϊt�룬����CQ.
(1)�����C�����ꣻ
(2)����OQC�ǵ���ֱ�������Σ���t��ֵΪ________��
(3)��CQƽ����OAC���������ֱ��CQ��Ӧ�ĺ�������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ�������̳�����һ�ָߵ�ˮ�������ÿǧ��ӯ��10Ԫ��ÿ����۳�500ǧ�ˣ����г����鷢�֣��ڽ����۲��������£���ÿǧ���Ǽ�1Ԫ����������������20ǧ�ˣ�
(1)�ָ��̳�Ҫ��֤ÿ��ӯ��6000Ԫ��ͬʱ��Ҫʹ�˿͵õ�ʵ�ݣ���ôÿǧ��Ӧ�Ǽ۶���Ԫ��
(2)ÿǧ��ˮ���Ǽ۶���Ԫʱ���̳�ÿ���õ��������õ���������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�һ�����ƻ���,֣���н�����������ɫ���г�������,��֪A�ͺŵ����г���B�ͺŵ����г��ĵ��۵�30Ԫ,��8��A�ͺŵ����г�����7��B�ͺŵ����г�����������ͬ.
(1)A,B�����ͺŵ����г��ĵ��۷ֱ��Ƕ���?
(2)������A,B�������г���600��,��A�ͺ����г�������������B�ͺ����г���һ��,�������һ����ʡǮ�ķ���,������÷�������Ҫ�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���г��ֽε�ƽ���ٶ���![]() ǧ��/Сʱ��δ���������٣�����ͬ��ʱ���ڣ��г��ֽ���ʻ
ǧ��/Сʱ��δ���������٣�����ͬ��ʱ���ڣ��г��ֽ���ʻ![]() ǧ�ף����ٺ��г����ֽζ���ʻ
ǧ�ף����ٺ��г����ֽζ���ʻ![]() ǧ�ף�
ǧ�ף�
��1�����г�ƽ�����ٶ���ǧ��/Сʱ��
��2�������ٺ��г���ƽ���ٶ���![]() ǧ��/Сʱ�������е�
ǧ��/Сʱ�������е�![]() Ϊ����ǧ�ף�
Ϊ����ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���A��x����������ϣ���B������Ϊ��0��4����BCƽ�֡�ABO��x���ڵ�C��2��0������P���߶�AB��һ�����㣨��P�����A��B�غϣ�������P��AB�Ĵ��߷ֱ���x�ύ�ڵ�D����y�ύ�ڵ�E��DFƽ�֡�PDO��y���ڵ�F�����D�ĺ�����Ϊt��
��1����ͼ1����0��t��2ʱ����֤��DF��CB��
��2����t��0ʱ����ͼ2�в�ȫͼ�Σ��ж�ֱ��DF��CB��λ�ù�ϵ����֤����Ľ��ۣ�
��3������M������Ϊ��4��-1�����ڵ�P�˶��Ĺ����У�����MCE�����������BCO�����![]() ��ʱ��ֱ��д����ʱ��E�����꣮
��ʱ��ֱ��д����ʱ��E�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ڽ���
�ڽ���![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��
��![]() ����
����![]() �İ뾶Ϊ�� ��
�İ뾶Ϊ�� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com