
【题目】关于![]() 的方程
的方程![]() .
.
(1)求证:方程总有实根;(2)若方程的根为正整数,求整数![]() 的值.
的值.
【答案】(1)见解析;(2)m的值为0,±1.
【解析】
1)当m=1时,原方程为一元一次方程,通过解方程可得出m=1时方程有实数根;当m≠1时,由根的判别式△=4(m-1)2≥0,可得出m≠1时方程有实数根.综上即可证出结论;
(2)当m=1时,原方程为一元一次方程,通过解方程可得出m=1符合题意;当m≠1时,利用因式分解法解方程可得出方程的根,由方程的根为正整数结合m为整数即可得出m的值,综上此题得解.
解:(1)当![]() 即
即![]() 时,
时,![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]()
![]() ,
,
∴方程有根.
综上,不论m为何值,方程总有实根.
(2)当![]() ,
,![]() 符合题意
符合题意
当![]() 时,不妨设方程两根为
时,不妨设方程两根为![]() .
.
由题知![]()
又![]() 均为正整数
均为正整数
∴![]() 为正整数且
为正整数且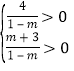
∴![]() ,2,4且
,2,4且![]()
∴![]()
综上m的值为0,±1.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() ,
,![]() 、
、![]() 、
、![]() 为常数)的图象如图所示,下列
为常数)的图象如图所示,下列![]() 个结论:①
个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 为常数,且
为常数,且![]() .其中正确的结论有( )
.其中正确的结论有( )
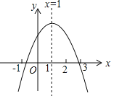
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,以线段
,以线段![]() 为直角边在第一象限内作等腰直角三角形
为直角边在第一象限内作等腰直角三角形![]() ,
,![]() ,点
,点![]() 为坐标系中的一个动点.
为坐标系中的一个动点.

(1)请直接写出直线![]() 的表达式;
的表达式;
(2)求出![]() 的面积;
的面积;
(3)当![]() 与
与![]() 面积相等时,求实数
面积相等时,求实数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
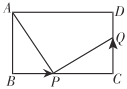
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,设点
运动,设点![]() 的运动时间为
的运动时间为![]() 秒,且
秒,且![]() .
.

(1)![]() _________
_________![]() (用含
(用含![]() 的代数式表示).
的代数式表示).
(2)如图,当点![]() 从点
从点![]() 开始运动的同时,点
开始运动的同时,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,是否存在这样的
运动,是否存在这样的![]() 值,使得以
值,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与以
为顶点的三角形与以![]() 、
、![]() 、
、![]() 为顶点的三角形全等?若存在,请求出v的值;若不存在,请说明理由.
为顶点的三角形全等?若存在,请求出v的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面立角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,点
,点![]() 在
在![]() 轴的负半轴上,若将
轴的负半轴上,若将![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 轴正半轴上的点
轴正半轴上的点![]() 处.
处.

(1)直接写出![]() 的长_________;
的长_________;
(2)求直线![]() 的函数表达式;
的函数表达式;
(3)求点![]() 和点
和点![]() 的坐标;
的坐标;
(4)![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() ?若存在,直接写出点
?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF.

(1)求证:DA∥BC;
(2)猜想线段DF、AF的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点B(7,6),顶点A、C在坐标轴上,矩形内部一点D在双曲线y=![]() 上,DE⊥AB于点E,DF⊥BC于点F,若四边形DEBF为正方形,则点D的坐标是( )
上,DE⊥AB于点E,DF⊥BC于点F,若四边形DEBF为正方形,则点D的坐标是( )

A. (2,6) B. (3,4) C. (4,3) D. (6,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
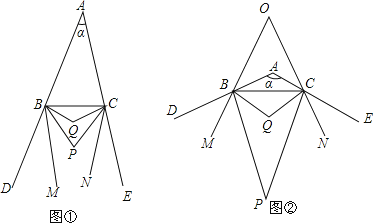
【题目】已知如图①,BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,BQ、CQ分别是∠PBC、∠PCB的角平分线,BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α.
(1)当α=40°时,∠BPC= °,∠BQC= °;
(2)当α= °时,BM∥CN;
(3)如图②,当α=120°时,BM、CN所在直线交于点O,求∠BOC的度数;
(4)在α>60°的条件下,直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com