
分析 (1)根据同分母分式的加法法则计算即可求解;
(2)先通分,再根据同分母分式的加减法法则计算即可求解;
(3)先通分,再根据同分母分式的减法法则计算即可求解;
(4)先约分,再通分,再根据同分母分式的加法法则计算即可求解.
解答 解:(1)$\frac{a-3b}{a-b}$+$\frac{a+b}{a-b}$
=$\frac{a-3b+a+b}{a-b}$
=2;
(2)$\frac{3c}{4{a}^{3}b}$-$\frac{a}{3{b}^{2}{c}^{2}}$+$\frac{4b}{9{a}^{2}{b}^{2}}$
=$\frac{9b{c}^{3}}{36{a}^{3}{b}^{2}{c}^{2}}$-$\frac{12{a}^{4}}{36{a}^{3}{b}^{2}{c}^{2}}$+$\frac{16ab{c}^{2}}{36{a}^{3}{b}^{2}{c}^{2}}$
=$\frac{9b{c}^{3}-12{a}^{4}+16ab{c}^{2}}{36{a}^{3}{b}^{2}{c}^{2}}$;
(3)$\frac{{x}^{2}+4x}{{x}^{2}+2x}$-$\frac{{x}^{2}-4}{{x}^{2}+4x+4}$
=$\frac{{x}^{2}+4x}{{x}^{2}+2x}$-$\frac{x-2}{x+2}$
=$\frac{{x}^{2}+4x-{x}^{2}+2x}{{x}^{2}+2x}$
=$\frac{6}{x+2}$;
(4)$\frac{{a}^{2}-4}{a+2}$+a+2
=$\frac{{a}^{2}-4+{a}^{2}+4a+4}{a+2}$
=2a.
点评 考查了分式的加减法,说明:①分式的通分必须注意整个分子和整个分母,分母是多项式时,必须先分解因式,分子是多项式时,要把分母所乘的相同式子与这个多项式相乘,而不能只同其中某一项相乘. ②通分是和约分是相反的一种变换.约分是把分子和分母的所有公因式约去,将分式化为较简单的形式;通分是分别把每一个分式的分子分母同乘以相同的因式,使几个较简单的分式变成分母相同的较复杂的形式.约分是对一个分式而言的;通分则是对两个或两个以上的分式来说的.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
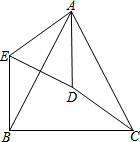 如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.
如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
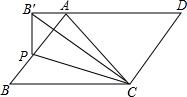 如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP长度为( )
如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP长度为( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
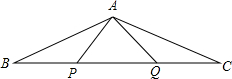 如图,P,Q是△ABC的边BC上的两点,且BP=QC=AP=AQ.
如图,P,Q是△ABC的边BC上的两点,且BP=QC=AP=AQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABOC中,对角线相交于点E,双曲线y=$\frac{k}{x}$(k<0)的一支经过C,E两点,若?ABCD的面积为10,求k的值.
如图,在?ABOC中,对角线相交于点E,双曲线y=$\frac{k}{x}$(k<0)的一支经过C,E两点,若?ABCD的面积为10,求k的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
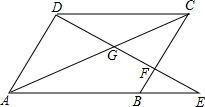 如图,四边形ABCD为平行四边形,试说明:
如图,四边形ABCD为平行四边形,试说明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com