
 如图,在?ABOC中,对角线相交于点E,双曲线y=$\frac{k}{x}$(k<0)的一支经过C,E两点,若?ABCD的面积为10,求k的值.
如图,在?ABOC中,对角线相交于点E,双曲线y=$\frac{k}{x}$(k<0)的一支经过C,E两点,若?ABCD的面积为10,求k的值. 分析 过点C作CD⊥x轴于点D,作CF⊥y轴于点F;过点E作EM⊥x轴于点M,作EN⊥y轴于点N,设点C的坐标为(m,$\frac{k}{m}$),点E的坐标为(n,$\frac{k}{n}$)(n<m<0).由四边形ABOC为平行四边形可得出“EN为梯形CFOB的中位线,EM为△BCD的中位线”,结合三角形中位线以及梯形中位线的性质可得出m、n的关系,由三角形的面积公式用m、n、k表示出S△OBC,再结合?ABCD的面积为10,即可求出k的值.
解答 解:过点C作CD⊥x轴于点D,作CF⊥y轴于点F;过点E作EM⊥x轴于点M,作EN⊥y轴于点N,如图所示.
设点C的坐标为(m,$\frac{k}{m}$),点E的坐标为(n,$\frac{k}{n}$)(n<m<0).
∵四边形ABOC为平行四边形,
∴BE=EC,EN为梯形CFOB的中位线,EM为△BCD的中位线.
∵CD=2EM,即-$\frac{k}{m}$=-2$\frac{k}{n}$,
∴n=2m.
∴OB=2EN-CF=-(2n-m)=-3m.
${S}_{△BOC}=\frac{1}{2}{S}_{平行四边形ABOC}$=$\frac{1}{2}$OB•CD=$\frac{1}{2}$×(-3m)•$\frac{k}{m}$=$\frac{1}{2}$×10=5,
解得:k=-$\frac{10}{3}$.
点评 本题考查了平行四边形的性质、三角形中位线的性质、梯形中位线的性质以及三角形的面积公式,解题的关键是找出m、n之间的关系.本题属于中档题,有点难度,解决该题型题目时,需要构建一个梯形,根据梯形与三角形中位线的性质用m、n表示出各边长,再结合三角形的面积公式求出k值.


科目:初中数学 来源: 题型:解答题
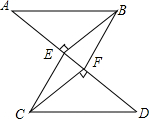 如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
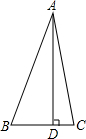 如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长(提示:运用轴对称知识,将图形进行翻折变换解答此题)
如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长(提示:运用轴对称知识,将图形进行翻折变换解答此题)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
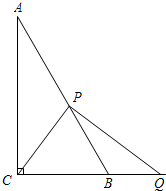 如图,在Rt△ABC中,∠C=90°,AB=6,P是射线AB上的一个动点,PQ⊥PC,交线段CB的延长线于点Q.
如图,在Rt△ABC中,∠C=90°,AB=6,P是射线AB上的一个动点,PQ⊥PC,交线段CB的延长线于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com